Elastic wave-mode separation for VTI media

Discussion

The separation of P and S wave-modes is based on the projection of elastic wavefields onto their respective polarization vectors. For VTI media, P and S mode polarization vectors can be conveniently obtained by solving the Christoffel equation. The Christoffel equation is a plane-wave solution to the elastic wave equation. Since the displacements, velocity and acceleration field have the same form of elastic wave equation, the separation algorithm applies to all these wavefields. The P and SV mode separation can be extended to TTI (transverse isotropy with a tilted symmetry axis) media by solving a TTI Christoffel matrix, and obtain TTI separators. Physically, the TTI media is just a rotation of VTI media.

In TI media, SV and SH waves are uncoupled most of the time, where SH wave is polarized out of plane. One only needs to decompose P and SV modes in the vertical plane. The plane wave solution is sufficient for most TI media, except for a special case where there exists a singularity point at an oblique propagation angle in the vertical plane (a line singularity in 3D), at which angle SV and SH wave velocities coincide. At this point, the SV wave polarization is not uniquely defined by Christoffel equation. S waves at the singularity are polarized in a plane orthogonal to the P wave polarization vector. However, this is not a problem since we define SV waves polarized in vertical planes only, therefore I remove the singularity by using the cylindrical coordinates. This situation is similar to S wave-mode coupling in orthorhombic media, where there is at least one singularity in a quadrant. However, as pointed out by Dellinger and Etgen (1990), the singularity in orthorhombic media is a global property of the media and cannot be removed, therefore the separation using polarization vectors in 3D orthorhombic media is not straightforward.

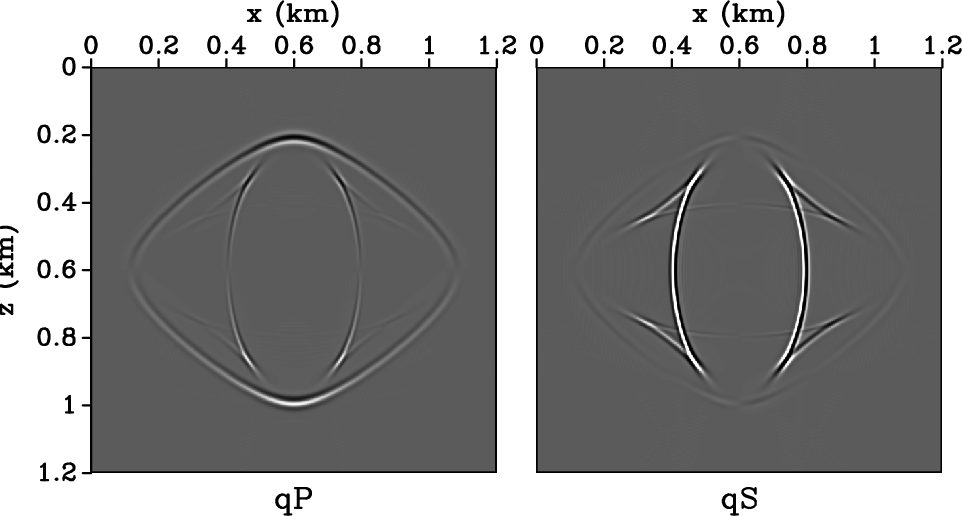
The anisotropic derivative operators depend on the anisotropic medium parameters. In Figure 19, I show how sensitive the separation is to the medium parameters. One elastic wavefield snapshot is shown in Figure 7(a) for a VTI medium with $V_{P0}/V_{S0}=2$ and $\epsilon=0.25$ , $\delta=-0.29$ . I try to separate the P and SV modes with (a) $\epsilon=0.4$ , $\delta=-0.1$ , (b) $\epsilon=0$ , $\delta=-0.3$ and (c) $\epsilon=0$ , $\delta=0$ . The separation shows that parameters (a) have good separation, showing the difference in $\epsilon$ and $\delta$ is important. The worst case scenario is shown by parameters (c), where isotropy is assumed for this VTI medium.

pA1,pA2,pA3
Figure 19. P and SV wave mode separation for a snapshot shown in Figure 7(a). The true medium parameters are $\epsilon=0.25$ , $\delta=-0.29$ . The separation assumes medium parameters of (a) $\epsilon=0.4$ , $\delta=-0.1$ , (b) $\epsilon=0$ , $\delta=-0.3$ , and (c) $\epsilon=0$ , $\delta=0$ . Hard clipping was applied to show the weak events. The plot shows that different estimate of anisotropy parameters has influence on the the wave mode separation.

Elastic wave-mode separation for VTI media