 |
 |
 |
 | Elastic wave-mode separation for VTI media |  |
![[pdf]](icons/pdf.png) |
Next: Operator properties
Up: Yan and Sava: VTI
Previous: Introduction
Separation of scalar and vector potentials can be achieved by
Helmholtz decomposition, which is applicable to any vector field
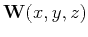 . By definition, the vector wavefield
. By definition, the vector wavefield 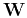 can be
decomposed into a curl-free scalar potential
can be
decomposed into a curl-free scalar potential 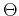 and a
divergence-free vector potential
and a
divergence-free vector potential
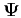 according to the
relation (Aki and Richards, 2002):
according to the
relation (Aki and Richards, 2002):
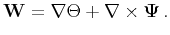 |
(1) |
Equation 1 is not used directly in practice, but the scalar and
vector components are obtained indirectly by the application of the
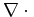 and
and
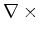 operators to the extrapolated elastic
wavefield:
operators to the extrapolated elastic
wavefield:
For isotropic elastic fields far from the source, quantities 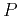 and
and
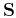 describe compressional and shear wave modes,
respectively (Aki and Richards, 2002).
describe compressional and shear wave modes,
respectively (Aki and Richards, 2002).
Equations 2 and 3 allow one to understand why
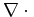 and
and
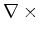 pass compressional and transverse wave modes, respectively. In the
discretized space domain, one can write:
pass compressional and transverse wave modes, respectively. In the
discretized space domain, one can write:
![$\displaystyle P= \nabla \cdot {\mathbf W} = D_x[W_x]+D_y[W_y]+D_z[W_z] ,$](img31.png) |
(4) |
where 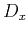 ,
, 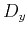 , and
, and 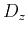 represent spatial derivatives in the
represent spatial derivatives in the
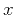 ,
, 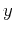 , and
, and 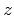 directions, respectively. Applying derivatives in
the space domain is equivalent to applying finite difference filtering
to the functions. Here,
directions, respectively. Applying derivatives in
the space domain is equivalent to applying finite difference filtering
to the functions. Here,
![$ D\left [\cdot\right]$](img37.png) represents spatial filtering of
the wavefield with finite difference operators. In the Fourier domain,
one can represent the operators
represents spatial filtering of
the wavefield with finite difference operators. In the Fourier domain,
one can represent the operators 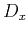 ,
, 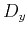 , and
, and 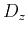 by
by 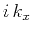 ,
,
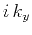 , and
, and 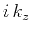 , respectively; therefore, one can write an
equivalent expression to equation 4 as:
, respectively; therefore, one can write an
equivalent expression to equation 4 as:
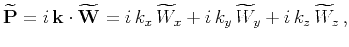 |
|
|
(5) |
where
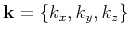 represents the wave vector, and
represents the wave vector, and
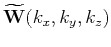 is the 3D Fourier transform of the wavefield
is the 3D Fourier transform of the wavefield
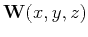 . We see that in this domain, the operator
. We see that in this domain, the operator
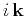 essentially projects the wavefield
essentially projects the wavefield
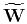 onto the wave vector
onto the wave vector 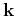 ,
which represents the polarization direction for P waves. Similarly,
the operator
,
which represents the polarization direction for P waves. Similarly,
the operator
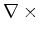 projects the wavefield onto the direction
orthogonal to the wave vector
projects the wavefield onto the direction
orthogonal to the wave vector 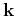 , which represents the polarization
direction for S waves (Dellinger and Etgen, 1990). For illustration,
Figure 1(a) shows the polarization vectors of the P mode of
a 2D isotropic model as a function of normalized
, which represents the polarization
direction for S waves (Dellinger and Etgen, 1990). For illustration,
Figure 1(a) shows the polarization vectors of the P mode of
a 2D isotropic model as a function of normalized 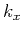 and
and 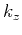 ranging
from
ranging
from 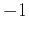 to
to 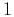 cycles. The polarization vectors are radial because the P
waves in an isotropic medium are polarized in the same directions as
the wave vectors.
cycles. The polarization vectors are radial because the P
waves in an isotropic medium are polarized in the same directions as
the wave vectors.


|
|---|
Iso-polarvector,Ani-polarvector
Figure 1. The qP and qS polarization vectors as a function of
normalized wavenumbers 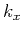 and
and 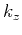 ranging from
ranging from 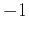 to
to 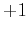 cycles, for (a) an isotropic model with
cycles, for (a) an isotropic model with 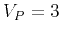 km/s and
km/s and
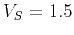 km/s, and (b) an anisotropic (VTI) model with
km/s, and (b) an anisotropic (VTI) model with
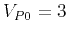 km/s,
km/s,
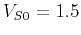 km/s,
km/s,
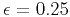 and
and
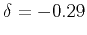 . The red arrows are the qP wave polarization vectors,
and the blue arrows are the qS wave polarization vectors.
. The red arrows are the qP wave polarization vectors,
and the blue arrows are the qS wave polarization vectors.
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[matlab]](icons/matlab.png) ![[matlab]](icons/matlab.png)
|
|---|
Dellinger and Etgen (1990) suggest the idea that wave mode separation
can be extended to anisotropic media by projecting the wavefields onto
the directions in which the P and S modes are polarized. This requires
that one should modify the wave separation equation 5 by projecting the
wavefields onto the true polarization directions U to obtain
quasi-P (qP) waves:
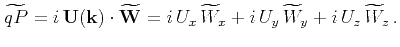 |
(6) |
In anisotropic media,
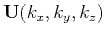 is different from
is different from 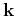 , as
illustrated in Figure 1(b), which shows the polarization
vectors of qP wave mode for a 2D VTI anisotropic model with normalized
, as
illustrated in Figure 1(b), which shows the polarization
vectors of qP wave mode for a 2D VTI anisotropic model with normalized
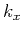 and
and 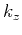 ranging from
ranging from 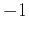 to
to 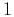 cycles. Polarization vectors are
not radial because qP waves in an anisotropic medium are not
polarized in the same directions as wave vectors, except in the
symmetry planes (
cycles. Polarization vectors are
not radial because qP waves in an anisotropic medium are not
polarized in the same directions as wave vectors, except in the
symmetry planes (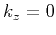 ) and along the symmetry axis (
) and along the symmetry axis (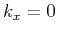 ).
).
Dellinger and Etgen (1990) demonstrate wave mode separation in
the wavenumber domain using projection of the polarization vectors,
as indicated in equation 6. However, for heterogeneous media, this
equation is defective because the polarization vectors are spatially
varying. One can write an equivalent expression to equation 6 in
the space domain for each grid point as:
![$\displaystyle {\it q}P=\nabla_a\cdot \mathbf W= L_x[W_x] + L_y[W_y] + L_z[W_z] ,$](img62.png) |
(7) |
where 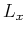 ,
, 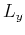 , and
, and 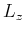 represent the inverse Fourier transforms
of
represent the inverse Fourier transforms
of 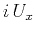 ,
, 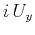 , and
, and 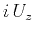 , respectively.
, respectively.
![$ L\left[\cdot\right]$](img69.png) represents spatial filtering of the wavefield
with anisotropic separators.
represents spatial filtering of the wavefield
with anisotropic separators. 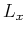 ,
, 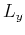 , and
, and 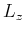 define the
pseudo derivative operators in the
define the
pseudo derivative operators in the 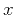 ,
, 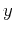 , and
, and 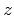 directions for an
anisotropic medium, respectively, and they change from location to
location according to the material parameters.
directions for an
anisotropic medium, respectively, and they change from location to
location according to the material parameters.
We obtain the polarization vectors
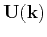 by solving the
Christoffel equation (Aki and Richards, 2002; Tsvankin, 2005):
by solving the
Christoffel equation (Aki and Richards, 2002; Tsvankin, 2005):
![$\displaystyle \left [{\bf G} - \rho V^2 {\bf I} \right]\mathbf U= 0 ,$](img71.png) |
(8) |
where G is the Christoffel matrix
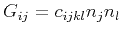 ,
in which
,
in which 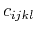 is the stiffness tensor,
is the stiffness tensor, 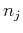 and
and 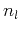 are the
normalized wave vector components in the
are the
normalized wave vector components in the 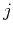 and
and 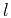 directions,
directions,
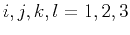 . The parameter
. The parameter 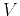 corresponds to the eigenvalues of
the matrix G. The eigenvalues
corresponds to the eigenvalues of
the matrix G. The eigenvalues 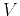 represent the phase
velocities of different wave modes and are functions of the wave vector
represent the phase
velocities of different wave modes and are functions of the wave vector
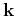 (corresponding to
(corresponding to 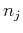 and
and 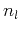 in the matrix G).
For plane waves propagating in any symmetry planes of a VTI medium,
one can set
in the matrix G).
For plane waves propagating in any symmetry planes of a VTI medium,
one can set 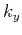 to 0
and get
to 0
and get
![$\displaystyle \left [ \mtrx{ c_{11} k_x^2 +c_{55} k_z^2 -\rho V^2 &0& \left (c_...
...c_{33} k_z^2 -\rho V^2 } \right] \left [\mtrx{ U_x\ U_y\ U_z} \right] =0 .$](img81.png) |
(9) |
The middle row of this matrix characterizes the SH wave
polarized in the 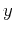 direction, and qP and qSV modes are
uncoupled from the SH mode and are polarized in the vertical
plane. The top and bottom rows of this equation
allow one to compute the polarization vector
direction, and qP and qSV modes are
uncoupled from the SH mode and are polarized in the vertical
plane. The top and bottom rows of this equation
allow one to compute the polarization vector
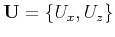 (the eigenvectors of the
matrix ) of P or SV wave mode
given the stiffness tensor at every location of the medium.
(the eigenvectors of the
matrix ) of P or SV wave mode
given the stiffness tensor at every location of the medium.
One can extend the procedure described here to heterogeneous media by
computing two different operator for each mode at every grid point. In the symmetry
planes of VTI media, the operators are 2D and depend on the local
values of the stiffness coefficients. For each point, I pre-compute
the polarization vectors as a function of the local medium parameters,
and transform them to the space domain to obtain the wave mode
separators. I assume that the medium parameters vary smoothly
(locally homogeneous), but even for complex media, the localized
operators work in the same way as the long finite difference operators.
If one represents the stiffness coefficients using Thomsen
parameters (Thomsen, 1986), then the pseudo derivative
operators 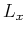 and
and 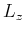 depend on
depend on 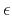 ,
, 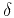 ,
, 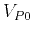 and
and
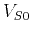 , which can be spatially varying
parameters. One can compute and store the operators for all grid points
in the medium, and then use these operators to separate P and S modes
from reconstructed elastic wavefields at different time steps. Thus,
wavefield separation in VTI media can be achieved simply by
non-stationary filtering with operators
, which can be spatially varying
parameters. One can compute and store the operators for all grid points
in the medium, and then use these operators to separate P and S modes
from reconstructed elastic wavefields at different time steps. Thus,
wavefield separation in VTI media can be achieved simply by
non-stationary filtering with operators 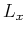 and
and 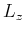 .
.
 |
 |
 |
 | Elastic wave-mode separation for VTI media |  |
![[pdf]](icons/pdf.png) |
Next: Operator properties
Up: Yan and Sava: VTI
Previous: Introduction
2013-08-29
![]() and
and
![]() pass compressional and transverse wave modes, respectively. In the
discretized space domain, one can write:
pass compressional and transverse wave modes, respectively. In the
discretized space domain, one can write:


![]() by solving the
Christoffel equation (Aki and Richards, 2002; Tsvankin, 2005):
by solving the
Christoffel equation (Aki and Richards, 2002; Tsvankin, 2005):
![]() and
and ![]() depend on
depend on ![]() ,
, ![]() ,
, ![]() and
and
![]() , which can be spatially varying
parameters. One can compute and store the operators for all grid points
in the medium, and then use these operators to separate P and S modes
from reconstructed elastic wavefields at different time steps. Thus,
wavefield separation in VTI media can be achieved simply by
non-stationary filtering with operators
, which can be spatially varying
parameters. One can compute and store the operators for all grid points
in the medium, and then use these operators to separate P and S modes
from reconstructed elastic wavefields at different time steps. Thus,
wavefield separation in VTI media can be achieved simply by
non-stationary filtering with operators ![]() and
and ![]() .
.