Consider the source point 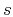 and the receiver point
and the receiver point 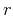 at the
surface
at the
surface 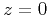 above a 2-D constant-velocity medium and a curved
reflector defined by the equation
above a 2-D constant-velocity medium and a curved
reflector defined by the equation 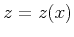 with a twice
differentiable function
with a twice
differentiable function 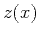 (Figure 1).
(Figure 1).
|
|---|
curve
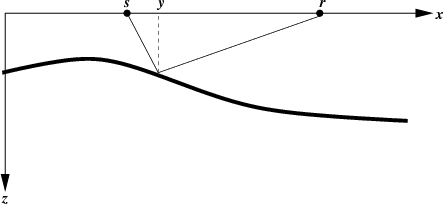
Figure 1. Geometry of reflection in a
constant-velocity medium with a curved reflector.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[xfig]](icons/xfig.png)
|
|---|
Note that the two-point ray trajectory can be parametrized by the
reflection point 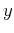 with the following expression for the
reflection traveltime (using the Pythagoras theorem):
with the following expression for the
reflection traveltime (using the Pythagoras theorem):
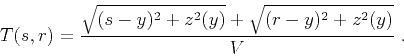 |
(10) |
- Apply Fermat's principle to specify
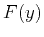 in the equation
in the equation
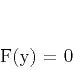 |
(11) |
required for finding the reflection point 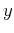 .
.
- Newton's method (successive linearization) solves nonlinear
equations like (11) iteratively by starting with some
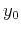 and repeating the iteration
and repeating the iteration
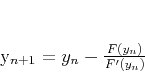 |
(12) |
for
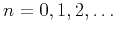
Specify 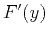 for the problem of finding the reflection point.
for the problem of finding the reflection point.
- Consider the special case of a dipping-plane reflector
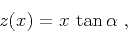 |
(13) |
where 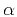 is the dip angle. Show that, in
this case, equation (11) reduces to a linear equation
for
is the dip angle. Show that, in
this case, equation (11) reduces to a linear equation
for 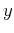 . Find
. Find 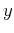 and substitute it into (10) to define the
reflection traveltime analytically.
and substitute it into (10) to define the
reflection traveltime analytically.
- (EXTRA CREDIT) Find the reflection traveltime for a circle reflector
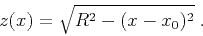 |
(14) |

![]() with the following expression for the
reflection traveltime (using the Pythagoras theorem):
with the following expression for the
reflection traveltime (using the Pythagoras theorem):
![]() for the problem of finding the reflection point.
for the problem of finding the reflection point.