Computational part

The first example is the model from Homework 1 with a hyperbolic reflector under a constant velocity layer. The model is shown in Figure 1. Figure 2 shows a shot gather modeled at the surface and extrapolated to a level of 1 km in depth using two extrapolation operators:

The exact phase shift filter

$\begin{displaymath} \hat{U}(z,k,\omega) = \hat{U}(0,k,\omega) e^{i \sqrt{S^2 \omega^2 - k^2} z}\;. \end{displaymath}$ (1)
Its approximation

$\begin{displaymath} \hat{U}(z,k,\omega) \approx \hat{U}(0,k,\omega) e^{i ... ... \left(\cos{(k \Delta x)}-1\right) z}{2 (\Delta x)^2}}\;. \end{displaymath}$ (2)

Approximation (2) is suitable for an implementation in the space domain with a digital recursive filter. However, its accuracy is limited, which is evident both from Figure 2 and from Figure 3, which compares the phases of the exact and the approximate extrapolators. We can see that approximation (2) is accurate only for small angles from the vertical $\theta$ , defined by

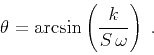
$\begin{displaymath} \theta = \arcsin\left(\frac{k}{S \omega}\right)\;. \end{displaymath}$

Your task: Design an approximation that would be more accurate than approximation (2). Your approximation should be suitable for a digital filter implementation in the space domain. Therefore, it can involve only through $\cos{(n k \Delta x)}$ functions with integer .

Change directory
```
cd hw5/hyper
```
Run
```
scons view
```
to generate figures and display them on your screen.
Edit the SConstruct file to change the approximate extrapolator.
Run
```
scons view
```
again to observe the differences.


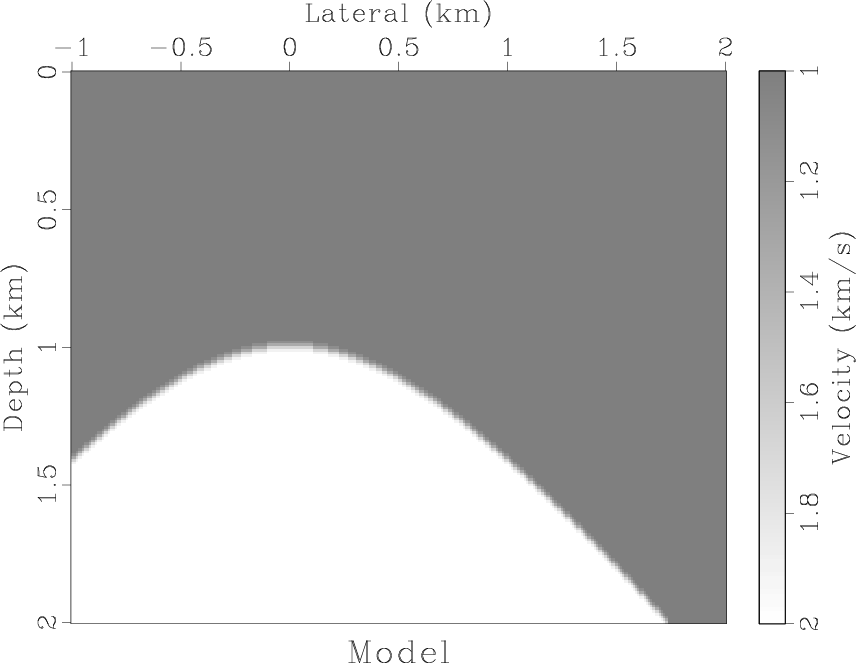
model Figure 1. Synthetic velocity model with a hyperbolic reflector.


shot Figure 2. Synthetic shot gather. Left: Modeled for receivers at the surface. Middle: Receivers extrapolated to 1 km in depth with an exact phase-shift extrapolation operator. Right: Receivers extrapolated to 1 km in depth with an approximate extrapolation operator.

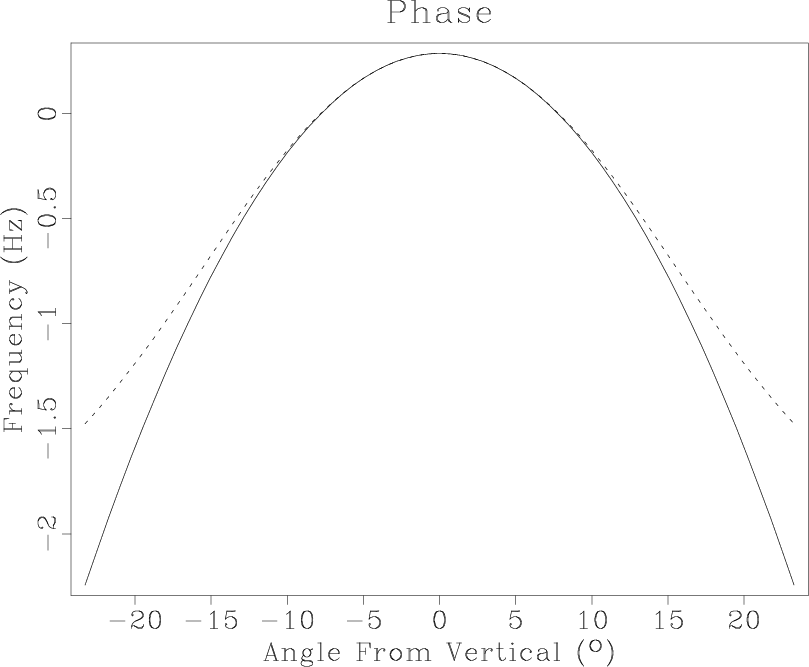
phase Figure 3. Phase of the extrapolation operator at 5 Hz frequency as a function of the wave propagation angle. Solid line: exact extrapolator. Dashed line: approximate extrapolator.

from rsf.proj import *
from math import pi

# Make a reflector model 
Flow('refl',None,
     '''
     math n1=10001 o1=-4 d1=0.001 output="sqrt(1+x1*x1)" 
     ''')
Flow('model','refl',
     '''
     unif2 n1=201 d1=0.01 v00=1,2 |
     put label1=Depth unit1=km label2=Lateral unit2=km
     label=Velocity unit=km/s | 
     smooth rect1=3
     ''')
Result('model',
       '''
       window min2=-1 max2=2 j2=10 |
       grey allpos=y title=Model 
       scalebar=y barreverse=y 
       ''')

# Reflector dip
Flow('dip','refl','math output="x1/input" ')

# Kirchoff modeling
Flow('shot','refl dip',
     '''
     kirmod nt=1501 twod=y vel=1 freq=10  
     ns=1 s0=1 ds=0.01 nh=801 dh=0.01 h0=-4
     dip=${SOURCES[1]} verb=y |
     costaper nw2=200
     ''')
Plot('shot',
     '''
     window min2=-2 max2=2 min1=1 max1=4 |
     grey title="0 km Depth" 
     label1=Time unit1=s label2=Offset unit2=km
     labelsz=10 titlesz=15 grid=y
     ''')

# Double Fourier transform

Flow('kw','shot','fft1 | fft3 axis=2')

# Extrapolation filters

dx = 0.01
dz = 1

dx2 = 2*pi*dx
dz2 = 2*pi*dz
a = 0.5*dz2/(dx2*dx2)

# In the expressions below,
# x1 refers to omega and x2 refers to k

Flow('exact','kw',
     'math output="exp(I*sqrt(x1*x1-x2*x2)*%g)" ' % dz2)

Flow('approximate','kw',
     '''
     window f1=1 |
     math output="exp(I*x1*%g)* 
     (x1+I*(cos(x2*%g)-1)*%g)/
     (x1-I*(cos(x2*%g)-1)*%g)" |
     pad beg1=1 
     ''' % (dz2,dx2,a,dx2,a))

# Extrapolation

for case in ('exact','approximate'):
    Flow('phase-'+case,case,
         '''
         window n1=1 min1=5 min2=-2 max2=2 | 
         math output="log(input)" | sfimag
         ''')
    Flow('angle-'+case,'phase-'+case,
         '''
         math output="%g*asin(x1/5)" |
         cmplx $SOURCE
         ''' % (180/pi))

    Flow('shot-'+case,['kw',case],
         '''
         mul ${SOURCES[1]} | 
         fft3 axis=2 inv=y | fft1 inv=y
         ''')
    Plot('shot-'+case,
         '''
         window min2=-2 max2=2 min1=1 max1=4 |
         grey title="%g km Depth (%s)" 
         label1=Time unit1=s label2=Offset unit2=km
         labelsz=10 titlesz=15 grid=y
         ''' % (dz, case.capitalize()))

Result('shot','shot shot-exact shot-approximate',
       'SideBySideAniso')

Result('phase','angle-exact angle-approximate',
       '''
       cat axis=2 ${SOURCES[1]} | 
       graph title=Phase dash=0,1 
       label1="Angle From Vertical" unit1="ô_"
       ''')

End()

Now we will approach the imaging task using reverse-time migration with a two-way wave extrapolation. Figure 4a shows synthetic zero-offset data generated by Kirchhoff modeling. Figure 4b shows an image generated by zero-offset reverse-time migration using an explicit finite-difference wave extrapolation in time.

Your task: Change the program for reverse-time migration to implement forward-time modeling using the ``exploding reflector'' approach.

Change directory
```
cd hw6/hyper2
```
Run
```
scons view
```
to generate figures and display them on your screen.
Run
```
scons wave.vpl
```
to observe a movie of reverse-time wave extrapolation.
Edit the program in the rtm.c file (or rtm.py) to implement a process opposite to migration: starting from the reflectivity image like the one in Figure 4b and generating zero-offset data like the one in Figure 4a.
Run
```
scons view
```
again to observe the differences.


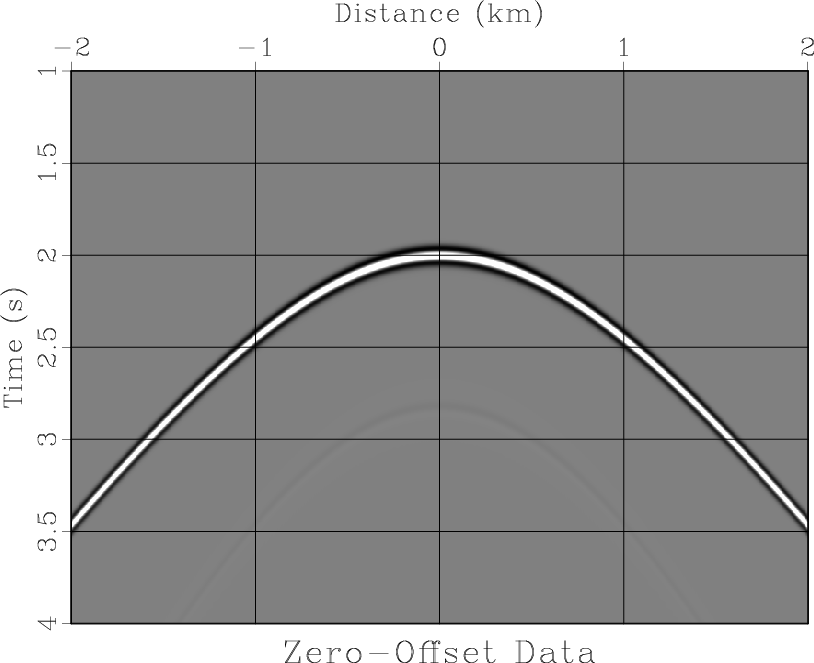
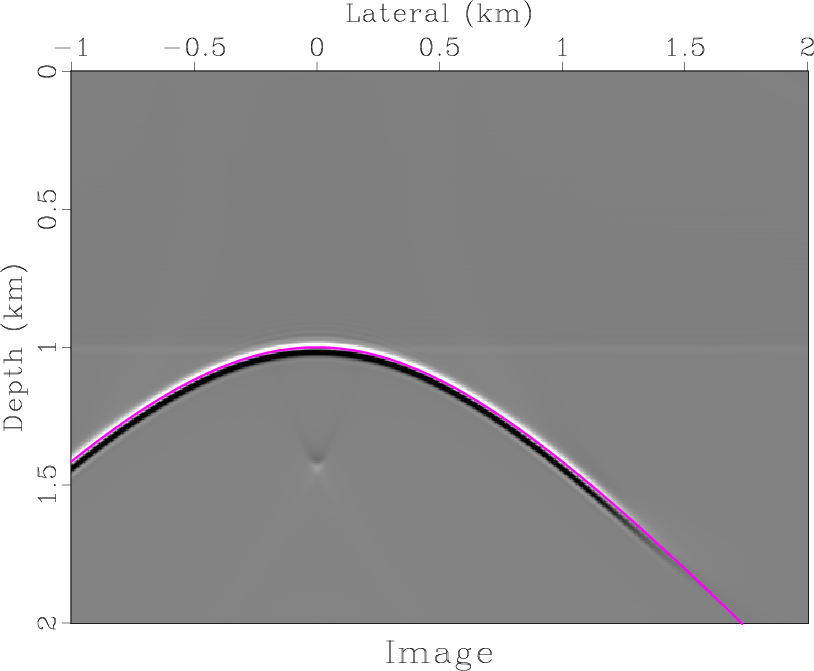
data,image Figure 4. (a) Synthetic zero-offset data corresponding to the model in Figure 1. (b) Image generated by reverse-time exploding-reflector migration. The location of the exact reflector is indicated by a curve.

from rsf.proj import *

# Make a reflector model 
Flow('refl',None,
     '''
     math n1=10001 o1=-4 d1=0.001 output="sqrt(1+x1*x1)" 
     ''')
Flow('model','refl',
     '''
     window min1=-3 max1=3 j1=5  |
     unif2 n1=401 d1=0.005 v00=1,2 |
     put label1=Depth unit1=km label2=Lateral unit2=km |
     smooth rect1=3
     ''')

Plot('model',
     '''
     window min2=-1 max2=2 |
     grey allpos=y bias=1 title=Model 
     ''')
Plot('refl',
     '''
     graph wanttitle=n wantaxis=n yreverse=y
     min1=-1 max1=2 min2=0 max2=2 
     plotfat=3 plotcol=4 
     ''') 
Result('model','model refl','Overlay')

# Kirchoff zero-offset modeling
Flow('dip','refl','math output="x1/input" ')

Flow('data','refl dip',
     '''
     kirmod nt=1501 dt=0.004 freq=10
     ns=1201 s0=-3 ds=0.005 nh=1 dh=0.01 h0=0
     twod=y vel=1 dip=${SOURCES[1]} verb=y |
     window | costaper nw2=200 
     ''')
Result('data',
     '''
     window min2=-2 max2=2 min1=1 max1=4 |
     grey title="Zero-Offset Data" grid=y 
     label1=Time unit1=s label2=Distance unit2=km
     ''')

# Reverse-time migration
proj = Project()

# To do the coding assignment in Python,
# comment the next line and uncomment the lines below
prog = proj.Program('rtm.c')

#prog = proj.Command('rtm.exe','rtm.py','cp $SOURCE $TARGET')
#AddPostAction(prog,Chmod(prog,0o755))

Flow('image wave','model %s data' % prog[0],
     '''
     pad beg1=200 end1=200 | math output=0.5 |
     ./${SOURCES[1]} data=${SOURCES[2]} 
     wave=${TARGETS[1]} jt=20 n0=200
     ''')

# Display wave propagation movie
Plot('wave',
     '''
     window min2=-1 max2=2 min1=0 max1=2 f3=33 |
     grey wanttitle=n gainpanel=all
     ''',view=1)

# Display image
Plot('image',
     '''
     window min2=-1 max2=2 min1=0 max1=2 |
     grey title=Image 
     ''')
Result('image','image refl','Overlay')

End()

/* 2-D zero-offset reverse-time migration */
#include <rsf.h>

#ifdef _OPENMP
#include <omp.h>
#endif

static int n1, n2;
static float c0, c11, c21, c12, c22;

static void laplacian(float **uin  /* [n2][n1] */, 
		      float **uout /* [n2][n1] */)
/* Laplacian operator, 4th-order finite-difference */
{
    int i1, i2;

#ifdef _OPENMP
#pragma omp parallel for	                       private(i2,i1)		                       shared(n2,n1,uout,uin,c11,c12,c21,c22,c0)
#endif	    
    for (i2=2; i2 < n2-2; i2++) {
	for (i1=2; i1 < n1-2; i1++) {
	    uout[i2][i1] = 
		c11*(uin[i2][i1-1]+uin[i2][i1+1]) +
		c12*(uin[i2][i1-2]+uin[i2][i1+2]) +
		c21*(uin[i2-1][i1]+uin[i2+1][i1]) +
		c22*(uin[i2-2][i1]+uin[i2+2][i1]) +
		c0*uin[i2][i1];
	}
    }
}

int main(int argc, char* argv[])
{
    int it,i1,i2;        /* index variables */
    int nt,n12,n0,nx, jt;
    float dt,dx,dz, dt2,d1,d2;

    float  **vv, **dd;          
    float  **u0,**u1,u2,**ud; /* tmp arrays */

    sf_file data, imag, modl, wave; /* I/O files */

    /* initialize Madagascar */
    sf_init(argc,argv);

    /* initialize OpenMP support */ 
    omp_init();

    /* setup I/O files */
    modl = sf_input ("in");   /* velocity model */
    imag = sf_output("out");  /* output image */
 
    data = sf_input ("data"); /* seismic data */
    wave = sf_output("wave"); /* wavefield */
    
    /* Dimensions */
    if (!sf_histint(modl,"n1",&n1)) sf_error("n1");
    if (!sf_histint(modl,"n2",&n2)) sf_error("n2");

    if (!sf_histfloat(modl,"d1",&dz)) sf_error("d1");
    if (!sf_histfloat(modl,"d2",&dx)) sf_error("d2");

    if (!sf_histint  (data,"n1",&nt)) sf_error("n1");
    if (!sf_histfloat(data,"d1",&dt)) sf_error("d1");

    if (!sf_histint(data,"n2",&nx) || nx != n2) 
	sf_error("Need n2=%d in data",n2);

    n12 = n1*n2;

    if (!sf_getint("n0",&n0)) n0=0;
    /* surface */
    if (!sf_getint("jt",&jt)) jt=1; 
    /* time interval */

    sf_putint(wave,"n3",1+(nt-1)/jt);
    sf_putfloat(wave,"d3",-jt*dt);
    sf_putfloat(wave,"o3",(nt-1)*dt);

    dt2 = dt*dt;

    /* set Laplacian coefficients */
    d1 = 1.0/(dz*dz);
    d2 = 1.0/(dx*dx);

    c11 = 4.0*d1/3.0;
    c12=  -d1/12.0;
    c21 = 4.0*d2/3.0;
    c22=  -d2/12.0;
    c0  = -2.0 * (c11+c12+c21+c22);

    /* read data and velocity */
    dd = sf_floatalloc2(nt,n2);
    sf_floatread(dd[0],nt*n2,data);

    vv = sf_floatalloc2(n1,n2);
    sf_floatread(vv[0],n12,modl);

    /* allocate temporary arrays */
    u0=sf_floatalloc2(n1,n2);
    u1=sf_floatalloc2(n1,n2);
    ud=sf_floatalloc2(n1,n2);
    
    for (i2=0; i2<n2; i2++) {
	for (i1=0; i1<n1; i1++) {
	    u0[i2][i1]=0.0;
	    u1[i2][i1]=0.0;
	    ud[i2][i1]=0.0;
	    vv[i2][i1] *= vv[i2][i1]*dt2;
	}
    }

    /* Time loop */
    for (it=nt-1; it >= 0; it-) {
	sf_warning("%d;",it);

	laplacian(u1,ud);

#ifdef _OPENMP
#pragma omp parallel for	         private(i2,i1,u2)		         shared(ud,vv,it,u1,u0,dd,n0)
#endif
	for (i2=0; i2<n2; i2++) {
	    for (i1=0; i1<n1; i1++) {
		/* scale by velocity */
		ud[i2][i1] *= vv[i2][i1];

		/* time step */
		u2 = 
		    2*u1[i2][i1] 
		    - u0[i2][i1] 
		    + ud[i2][i1]; 
		
		u0[i2][i1] = u1[i2][i1];
		u1[i2][i1] = u2;
	    }

	    /* inject data */
	    u1[i2][n0] += dd[i2][it];
	}

	if (0 == it%jt) 
	    sf_floatwrite(u1[0],n12,wave);       
    }
    sf_warning(".");	

    /* output image */
    sf_floatwrite(u1[0],n12,imag);
    
    exit (0);
}

#!/usr/bin/env python

import sys
import numpy
import m8r

class Laplacian:
    'Laplacian operator, 4th-order finite-difference'
    
    def __init__(self,d1,d2):
        self.c11 = 4.0*d1/3.0
        self.c12=  -d1/12.0
        self.c21 = 4.0*d2/3.0
        self.c22=  -d2/12.0
        self.c1  = -2.0*(self.c11+self.c12)
        self.c2  = -2.0*(self.c21+self.c22)
    
    def apply(self,uin,uout):
        n1,n2 = uin.shape
    
        uout[2:n1-2,2:n2-2] =           self.c11*(uin[1:n1-3,2:n2-2]+uin[3:n1-1,2:n2-2]) +           self.c12*(uin[0:n1-4,2:n2-2]+uin[4:n1  ,2:n2-2]) +           self.c1*uin[2:n1-2,2:n2-2] +           self.c21*(uin[2:n1-2,1:n2-3]+uin[2:n1-2,3:n2-1]) +           self.c22*(uin[2:n1-2,0:n2-4]+uin[2:n1-2,4:n2  ]) +           self.c2*uin[2:n1-2,2:n2-2]

par = m8r.Par()

# setup I/O files
modl=m8r.Input()       # velocity model
imag=m8r.Output()      # output image

data=m8r.Input ('data') # seismic data
wave=m8r.Output('wave') # wavefield

# Dimensions
n1 = modl.int('n1')
n2 = modl.int('n2')

dz = modl.float('d1')
dx = modl.float('d2')

nt = data.int('n1')
dt = data.float('d1')

nx = data.int('n2')
if nx != n2:
    raise RuntimeError('Need n2=%d in data',n2)

n0 = par.int('n0',0) # surface
jt = par.int('jt',1) # time interval

wave.put('n3',1+(nt-1)/jt)
wave.put('d3',-jt*dt)
wave.put('o3',(nt-1)*dt)

dt2 =    dt*dt

# set Laplacian coefficients 
laplace = Laplacian(1.0/(dz*dz),1.0/(dx*dx))

# read data and velocity
dd = numpy.zeros([n2,nt],'f')
data.read(dd)
vv = numpy.zeros([n2,n1],'f')
modl.read(vv)

# allocate temporary arrays
u0 = numpy.zeros([n2,n1],'f')
u1 = numpy.zeros([n2,n1],'f')
ud = numpy.zeros([n2,n1],'f')

vv *= vv*dt2

# Time loop
for it in range(nt-1,-1,-1):
    sys.stderr.write("%d" % it)
    
    laplace.apply(u1,ud)

    # scale by velocity
    ud *= vv

    # time step 
    u2 = 2*u1 - u0 + ud 
    u0 = u1
    u1 = u2

    # inject data
    u1[:,n0] += dd[:,it]

    if 0 == it%jt:
        wave.write(u1)

# output image
imag.write(u1)

Figure 5 shows the Sigsbee velocity model and its an approximate filtered reflectivity.


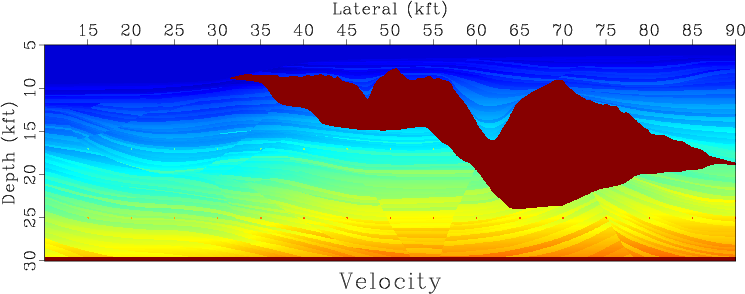
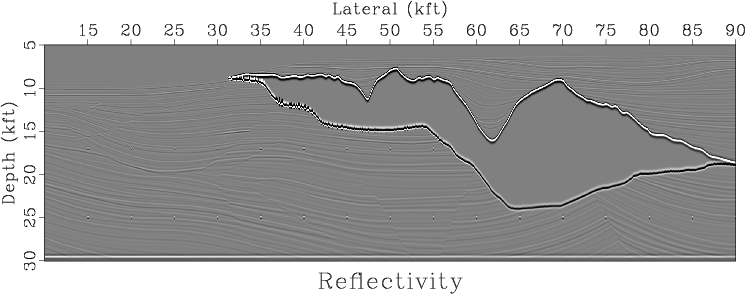
zvel,zref Figure 5. (a) Sigsbee velocity model. (b) Approximate reflectivity of the Sigsbee model (an ideal image).

Your task: Apply your exploding-reflector modeling and migration program from the previous task to generate zero-offset data for Sigsbee and image it.

Change directory
```
cd hw6/sigsbee
```
Run
```
scons view
```
to generate figures and display them on your screen.
Modify the SConstruct file to implement the modeling and migration experiment.
Include your results in the paper by editing the hw6/paper.tex file.

from rsf.proj import *

# Download velocity model from the data server
##############################################
vstr = 'sigsbee2a_stratigraphy.sgy'
Fetch(vstr,'sigsbee')
Flow('zvstr',vstr,'segyread read=data')

Flow('zvel','zvstr',
     '''
     put d1=0.025 o2=10.025 d2=0.025
     label1=Depth unit1=kft label2=Lateral unit2=kft |
     scale dscale=0.001
     ''')

Result('zvel',
       '''
       window f1=200 |
       grey title=Velocity titlesz=7 color=j
       screenratio=0.3125 screenht=4 labelsz=5
       mean=y
       ''')

# Compute approximate reflectivity
##################################
Flow('zref','zvel',
     '''
     depth2time velocity=$SOURCE nt=2501 dt=0.004 |
     ai2refl | ricker1 frequency=10 |
     time2depth velocity=$SOURCE
     ''')

Result('zref',
       '''
       window f1=200 |
       grey title=Reflectivity titlesz=7
       screenratio=0.3125 screenht=4 labelsz=5
       ''')

End()

We return to the synthetic model shown in Figure 6a to experiment with modeling and migration by the phase-shift method in a

medium.

Figure 6b shows an idealized image (band-passed reflectivity) for the synthetic model. In ``exploding-reflector'' modeling, this image is assumed to be the seismic wavefield frozen at zero time. The modeling program extrapolates the wavefield to the surface and is implemented in phaseshift.c. The program operates in the frequency-wavenumber domain and establishes a linear relationship between reflectivity as a function of depth and zero-offset data as a function of frequency for one space wavenumber. If we think of this linear relationship as a matrix multiplication, we can associate forward modeling with multiplication

$\begin{displaymath} \mathbf{d} = \mathbf{A} \mathbf{m} \end{displaymath}$

(3)

and migration with the adjoint multiplication

$\begin{displaymath} \widehat{\mathbf{m}} = \mathbf{A}^T \mathbf{d}\;, \end{displaymath}$

(4)

where $\mathbf{A}^T$ is the conjugate transpose of $\mathbf{A}$ .

Figure 7 shows the result of forward modeling (multiplication by $\mathbf{A}$ ) after inverse Fourier transform to time and space. Your task is to implement the corresponding migration (multiplication by $\mathbf{A}^T$ ).

Instead of simply applying the adjoint operator, we can also try to compute the least-squares inverse

$\begin{displaymath} \widehat{\mathbf{m}} = \left(\mathbf{A}^T \mathbf{A}\right)^{-1} \mathbf{A}^T \mathbf{d}\;, \end{displaymath}$

(5)

which corresponds to the minimum of the least-squares misfit function $\vert\mathbf{A} \mathbf{m}-\mathbf{d}\vert^2$ . In practice, inversion in equation (5) is implemented with an iterative conjugate-gradient algorithm, which applies $\mathbf{A}$ and $\mathbf{A}^T$ (modeling and migration) at each iteration without the need to form any matrices explicitly.


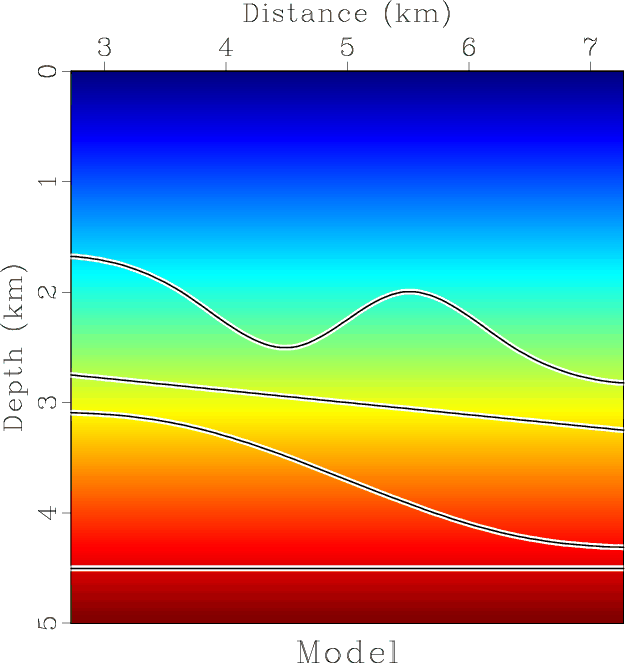
lmodel,expl Figure 6. (a) Synthetic model: curved reflectors in a velocity. (b) ``Exploding reflector'', an ideal image of band-passed reflectivity.


modl Figure 7. Zero-offset data generated by exploding-reflector phase-shift modeling.

Change directory
```
cd hw5/lsmig
```
Run
```
scons view
```
to generate the figures and display them on your screen.
Modify the program in the phaseshift.c file to fill the missing part and to implement phase-shift migration as the adjoint of phase-shift modeling.
Modify the SConstruct file to uncomment the part related to migration. Check your result by running
```
scons migr.view
```
Test if your migration code is truly the adjoint of modeling by running the dot-product test
```
sfcdottest ./phaseshift.exe mod=kexpl.rsf dat=kmodl.rsf \
vel=vofz.rsf nw=247 dw=0.16276
```
On a machine with multiple CPUs, you can also try
```
sfcdottest sfomp ./phaseshift.exe split=2 \
mod=kexpl.rsf dat=kmodl.rsf vel=vofz.rsf nw=247 dw=0.16276
```
If your adjoint is correct, you should see two identical sets of numbers, such as
```
sfcdottest:  L[m]*d=(25264,-20273.9)
sfcdottest: L'[d]*m=(25264,-20273.9)
```
Your actual numbers will be different because of random input vectors but they should be the same between L[m]*d and L'[d]*m.
Now you are ready for testing least-squares migration. Uncomment the corresponding lines in SConstruct and run
```
scons invs.view
```
Do you notice any difference with the previous result? Increase the number of iterations from 10 to 100 and repeat the experiment.
Include your figures in this document by editing hw5/paper.tex.
For EXTRA CREDIT, use two-way wave extrapolation from the previous part to implement least-squares exploding-reflector reverse-time migration and apply it to the Sigsbee model.

from rsf.proj import *

# Generate a reflector model

layers = (
     ((0,2),(3.5,2),(4.5,2.5),(5,2.25),
       (5.5,2),(6.5,2.5),(10,2.5)),
     ((0,2.5),(10,3.5)),
     ((0,3.2),(3.5,3.2),(5,3.7),
       (6.5,4.2),(10,4.2)),
     ((0,4.5),(10,4.5))
)

nlays = len(layers)
for i in range(nlays):
     inp = 'inp%d' % i
     Flow(inp+'.asc',None,
          '''
          echo %s in=$TARGET
          data_format=ascii_float n1=2 n2=%d
          ''' %            (' '.join(map(lambda x: ' '.join(map(str,x)),
                           layers[i])),len(layers[i])))

dim1 = 'o1=0 d1=0.05 n1=201'
Flow('lay1','inp0.asc',
     'dd form=native | spline %s fp=0,0' % dim1)
Flow('lay2',None  ,
     'math %s output="2.5+x1*0.1" '      % dim1)
Flow('lay3','inp2.asc',
     'dd form=native | spline %s fp=0,0' % dim1)
Flow('lay4',None  ,'math %s output=4.5'  % dim1)

Flow('lays','lay1 lay2 lay3 lay4',
     'cat axis=2 ${SOURCES[1:4]}')

graph = '''
graph min1=2.5 max1=7.5 min2=0 max2=5
yreverse=y wantaxis=n wanttitle=n screenratio=1
'''
Plot('lays0','lays',graph + ' plotfat=10 plotcol=0')
Plot('lays1','lays',graph + ' plotfat=2 plotcol=7')
Plot('lays2','lays',graph + ' plotfat=2')

# Velocity

Flow('vofz',None,
     '''
     math output="1.5+0.25*x1"
     d2=0.05 n2=201 d1=0.01 n1=501
     label1=Depth unit1=km
     label2=Distance unit2=km
     label=Velocity unit=km/s
     ''')
Plot('vofz',
     '''
     window min2=2.75 max2=7.25 |
     grey color=j allpos=y bias=1.5
     title=Model screenratio=1
     ''')

Result('lmodel','vofz lays0 lays1','Overlay')

# Exploding reflector

Flow('expl','lays vofz',
     '''
     unif2 d1=0.01 n1=501 v00=1,2,3,4,5 |
     depth2time velocity=${SOURCES[1]} |
     ai2refl | ricker1 frequency=10 |
     time2depth velocity=${SOURCES[1]} |
     put label1=Depth unit1=km 
     label2=Distance unit2=km
     ''')

Result('expl',
       '''
       window max1=5 min2=2.5 max2=7.5 | 
       grey title="Exploding Reflector" screenratio=1
       ''')

# Modeling
##########

proj = Project()
prog = proj.Program('phaseshift.c')

# Cosine Fourier transform
Flow('kexpl','expl','cosft sign2=1 | rtoc')

Flow('kmodl','kexpl %s vofz' % prog[0],
     '''
     ./${SOURCES[1]} vel=${SOURCES[2]} 
     nw=247 dw=0.16276
     ''')

Flow('modl','kmodl',
     'pad n1=769 | fft1 inv=y | cosft sign2=-1')

Result('modl',
       '''
       grey title="Exploding Reflector Modeling" 
       label1=Time unit1=s
       ''')

# Migration
###########

Flow('kdata','modl',
     'cosft sign2=1 | fft1 | window n1=247')

Flow('kmigr','kdata %s vofz' % prog[0],
     './${SOURCES[1]} vel=${SOURCES[2]} adj=1')

Flow('migr','kmigr','real | cosft sign2=-1')

# !!! UNCOMMENT BELOW !!!

#Result('migr',
#       '''
#       window max1=5 min2=2.5 max2=7.5 | 
#       grey title="Exploding Reflector Migration" 
#       screenratio=1 label1=Depth unit1=km
#       ''')

# Least-Squares Migration
#########################

Flow('kinvs','kdata %s vofz kmigr' % prog[0],
     '''
     cconjgrad ./${SOURCES[1]} split=2 
     nw=247 dw=0.16276
     vel=${SOURCES[2]} mod=${SOURCES[3]} niter=10
     ''')

Flow('invs','kinvs','real | cosft sign2=-1')

# !!! UNCOMMENT BELOW !!!

#Result('invs',
#       '''
#       window max1=5 min2=2.5 max2=7.5 | 
#       grey title="Exploding Reflector LS Migration" 
#       screenratio=1 label1=Depth unit1=km
#       ''')


End()

/* Phase-shift modeling and migration */

#include <rsf.h>

int main(int argc, char* argv[])
{
    bool adj;
    int ik, iw, nk, nw, iz, nz;
    float k, dk, k0, dw, dz, z0, *v, eps;
    sf_complex *dat, *mod, w2, ps, wave;
    sf_file inp, out, vel;

    sf_init(argc,argv);

    if (!sf_getbool("adj",&adj)) adj=false;
    /* adjoint flag, 0: modeling, 1: migration */

    inp = sf_input("in");
    out = sf_output("out");
    vel = sf_input("vel"); /* velocity file */

    if (!sf_histint(vel,"n1",&nz)) 
	sf_error("No n1= in vel");
    if (!sf_histfloat(vel,"d1",&dz)) 
	sf_error("No d1= in vel");
    if (!sf_histfloat(vel,"o1",&z0)) z0=0.0;
    
    if (!sf_histint(inp,"n2",&nk)) 
	sf_error("No n2= in input");
    if (!sf_histfloat(inp,"d2",&dk)) 
	sf_error("No d2= in input");
    if (!sf_histfloat(inp,"o2",&k0)) 
	sf_error("No o2= in input");

    dk *= 2*SF_PI;
    k0 *= 2*SF_PI;

    if (adj) { /* migration */
	if (!sf_histint(inp,"n1",&nw)) 
	    sf_error("No n1= in input");
	if (!sf_histfloat(inp,"d1",&dw)) 
	    sf_error("No d1= in input");

	sf_putint(out,"n1",nz);
	sf_putfloat(out,"d1",dz);
	sf_putfloat(out,"o1",z0);
    } else {  /* modeling */
	if (!sf_getint("nw",&nw)) sf_error("No nw=");
	if (!sf_getfloat("dw",&dw)) sf_error("No dw=");

	sf_putint(out,"n1",nw);
	sf_putfloat(out,"d1",dw);
	sf_putfloat(out,"o1",0.0);	
    }

    if (!sf_getfloat("eps",&eps)) eps = 1.0f;
    /* stabilization parameter */

    dw *= 2*SF_PI;

    dat = sf_complexalloc(nw);
    mod = sf_complexalloc(nz);
    
    /* read velocity, convert to slowness squared */
    v = sf_floatalloc(nz);
    sf_floatread(v,nz,vel);
    for (iz=0; iz < nz; iz++) { 
	v[iz] = 2.0f/v[iz];
	v[iz] *= v[iz];
    }

    for (ik=0; ik<nk; ik++) { /* wavenumber */
	sf_warning("wavenumber %d of %d;",ik+1,nk);
	k=k0+ik*dk;
	k *= k;
	
	if (adj) {
	    sf_complexread(dat,nw,inp);
	    for (iz=0; iz < nz; iz++) { 
		mod[iz]=sf_cmplx(0.0,0.0);
	    }
	} else {
	    sf_complexread(mod,nz,inp);
	}

	for (iw=0; iw<nw; iw++) { /* frequency */
	    w2 = sf_cmplx(eps*dw,iw*dw);
	    w2 *= w2;

	    if (adj) { /* migration */
		wave = dat[iw];
		for (iz=0; iz < nz; iz++) { 
		    /* !!! FILL MISSING LINES !!! */
		}
	    } else {  /* modeling */
		wave = mod[nz-1];
		for (iz=nz-2; iz >=0; iz-) {
		    ps = cexpf(-csqrt(w2*v[iz]+k)*dz);
		    wave = wave*ps+mod[iz];
		}
		dat[iw] = wave;
	    }
	}
	
	if (adj) {
	    sf_complexwrite(mod,nz,out);
	} else {
	    sf_complexwrite(dat,nw,out);
	}
    } 
    sf_warning(".");

    exit(0);
}