 |
 |
 |
 | Seismic dip estimation based on the two-dimensional Hilbert transform and its application in random noise attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Synthetic data tests
Up: theory
Previous: Noniterative local dip calculation
Traditional stationary regression is used to estimate the coefficients
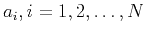 by minimizing the prediction error between a
``master'' signal s(
by minimizing the prediction error between a
``master'' signal s(
 ) (where
) (where
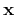 represents the
coordinates of a multidimensional space) and a collection of slave
signals
represents the
coordinates of a multidimensional space) and a collection of slave
signals
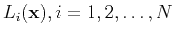 (Fomel, 2009)
(Fomel, 2009)
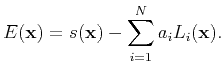 |
(7) |
When
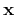 is 1D and
is 1D and 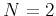 ,
,
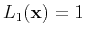 and
and
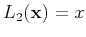 , the problem of minimizing
, the problem of minimizing
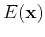 amounts to fitting a straight line
amounts to fitting a straight line
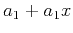 to the master
signal. Nonstationary regression is similar to equation 7
but allows the coefficients
to the master
signal. Nonstationary regression is similar to equation 7
but allows the coefficients
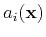 to vary with
to vary with
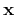 , and the error
(Fomel, 2009)
, and the error
(Fomel, 2009)
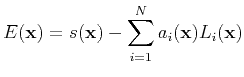 |
(8) |
is minimized to solve for the multinomial coefficients
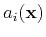 . The
minimization becomes an ill-posed problem because
. The
minimization becomes an ill-posed problem because
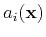 rely on
the independent variables
rely on
the independent variables
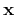 . To solve the ill-posed problem, we
constrain the coefficients
. To solve the ill-posed problem, we
constrain the coefficients
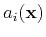 . Tikhonov's regularization
(Tikhonov, 1963) is a classical regularization method that amounts
to the minimization of the following functional (Fomel, 2009)
. Tikhonov's regularization
(Tikhonov, 1963) is a classical regularization method that amounts
to the minimization of the following functional (Fomel, 2009)
![$\displaystyle F(a)=\Vert E(\mathbf{x})\Vert^{2}+ \varepsilon^{2}\sum_{i=1}^{N}\Vert\mathbf{D}[a_{i}(\mathbf{x})]\Vert^2 ,$](img49.png) |
(9) |
where
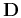 is the regularization operator and
is the regularization operator and
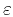 is
a scalar regularization parameter. When
is
a scalar regularization parameter. When
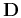 is a linear
operator, the least-squares estimation reduces to linear inversion
(Fomel, 2009)
is a linear
operator, the least-squares estimation reduces to linear inversion
(Fomel, 2009)
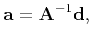 |
(10) |
where
and the elements of matrix
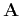 are
are

|
|---|
compare
Figure 2. Least-squares linear fitting
compared with nonstationary polynomial fitting.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
Next, we use a simple signal to simulate the variation of the
amplitude of a nonstationary event with random noise (dashed line in
Figure 2). In Figure 2, the dot dashed
line denotes the results of the least-squares linear fitting and the
solid line denotes the results of the nonstationary polynomial
fitting. We compare the least-squares linear fitting and nonstationary
polynomial fitting results, and we find that the nonstationary
polynomial fitting models the curve variations more accurately for
events with variable amplitude, particularly for  .
.
 |
 |
 |
 | Seismic dip estimation based on the two-dimensional Hilbert transform and its application in random noise attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Synthetic data tests
Up: theory
Previous: Noniterative local dip calculation
2015-05-07
![\begin{displaymath}\begin{split}\mathbf{a} & =[a_1(x)a_2(x)\cdots a_N(x)]^T ,\\ ...
...bf{d} & =[L_1(x)s(x)L_2(x)s(x)\cdots L_N(x)s(x)]^T, \end{split}\end{displaymath}](img52.png)

![]() .
.