 |
 |
 |
 | Multi-dimensional Fourier transforms in the helical coordinate
system |  |
![[pdf]](icons/pdf.png) |
Next: Speed comparison
Up: Theory
Previous: Linking 1-D and 2-D
With the understanding that the 1-D FFT of a multi-dimensional signal
in helical coordinates is equivalent to the 2-D FFT, a natural
question to ask is: how does the helical wavenumber, 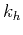 , relate to
spatial wavenumbers,
, relate to
spatial wavenumbers, 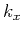 and
and 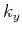 ?
?
The helical delay operator, 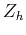 , is related to
, is related to 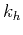 through the equation,
through the equation,
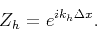 |
(8) |
In the discrete frequency domain this becomes
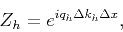 |
(9) |
where 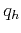 is the integer frequency index that lies in the range,
is the integer frequency index that lies in the range,
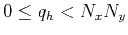 .
The uncertainty relationship,
.
The uncertainty relationship,
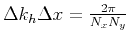 , allows this to be
simplified still further, leaving
, allows this to be
simplified still further, leaving
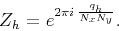 |
(10) |
If we find a form of 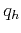 in terms of Fourier indices,
in terms of Fourier indices,
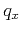 and
and 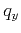 , that can be plugged into equation (10)
in order to satisfy equations (4)
and (5), this will provide the link between
, that can be plugged into equation (10)
in order to satisfy equations (4)
and (5), this will provide the link between 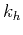 and
spatial wavenumbers,
and
spatial wavenumbers, 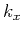 and
and 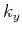 .
.
The idea that 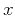 -axis wavenumbers will have a higher frequency than
-axis wavenumbers will have a higher frequency than
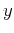 -axis wavenumbers, leads us to try a
-axis wavenumbers, leads us to try a 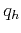 of the form,
of the form,
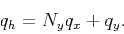 |
(11) |
Substituting this into equation (10) leads to
Since 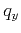 is bounded by
is bounded by 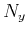 , for large
, for large 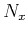 the second term in
braces
the second term in
braces
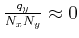 , and this
reduces to
, and this
reduces to
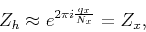 |
(14) |
which satisfies equation (4).
Substituting equation (11) into
equation (10), and raising it to the power of 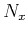 leads
to:
leads
to:
Since 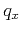 is an integer,
is an integer,
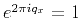 , and this reduces to
, and this reduces to
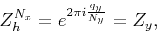 |
(17) |
which satisfies equation (5).
Equation (11), therefore, provides the link we are
looking for between 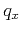 ,
, 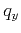 , and
, and 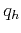 . It is interesting to
note that not only is there a one-to-one mapping between 1-D and 2-D
Fourier components, but equation (11) describes helical
boundaries in Fourier space: however, rather than wrapping around the
. It is interesting to
note that not only is there a one-to-one mapping between 1-D and 2-D
Fourier components, but equation (11) describes helical
boundaries in Fourier space: however, rather than wrapping around the
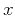 -axis as it does in physical space, the helix wraps around the
-axis as it does in physical space, the helix wraps around the
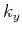 -axis in Fourier space (Figure 2). This provides
the link that is missing in Figure 1, but shown in
Figure 3.
-axis in Fourier space (Figure 2). This provides
the link that is missing in Figure 1, but shown in
Figure 3.
transp
Figure 2. Fourier dual of helical boundary
conditions is also helical boundary conditions with axis of helix
transposed.
|

|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[xfig]](icons/xfig.png)
|
|---|
ill2
Figure 3. Relationship between 1-D and 2-D
convolution, FFT's and the helix, illustrating the Fourier dual of
helical boundary conditions.
|

|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[xfig]](icons/xfig.png)
|
|---|
As with helical coordinates in physical space,
equation (11) can easily be inverted to yield
where ![$[x]$](img61.png) denotes the integer part of
denotes the integer part of 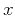 .
.
 |
 |
 |
 | Multi-dimensional Fourier transforms in the helical coordinate
system |  |
![[pdf]](icons/pdf.png) |
Next: Speed comparison
Up: Theory
Previous: Linking 1-D and 2-D
2013-03-03
![]() , is related to
, is related to ![]() through the equation,
through the equation,
![]() -axis wavenumbers will have a higher frequency than
-axis wavenumbers will have a higher frequency than
![]() -axis wavenumbers, leads us to try a
-axis wavenumbers, leads us to try a ![]() of the form,
of the form,
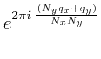
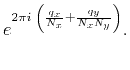
![]() leads
to:
leads
to:
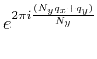
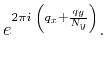
![]() ,
, ![]() , and
, and ![]() . It is interesting to
note that not only is there a one-to-one mapping between 1-D and 2-D
Fourier components, but equation (11) describes helical
boundaries in Fourier space: however, rather than wrapping around the
. It is interesting to
note that not only is there a one-to-one mapping between 1-D and 2-D
Fourier components, but equation (11) describes helical
boundaries in Fourier space: however, rather than wrapping around the
![]() -axis as it does in physical space, the helix wraps around the
-axis as it does in physical space, the helix wraps around the
![]() -axis in Fourier space (Figure 2). This provides
the link that is missing in Figure 1, but shown in
Figure 3.
-axis in Fourier space (Figure 2). This provides
the link that is missing in Figure 1, but shown in
Figure 3.


![$\displaystyle \Delta k_x q_x = \frac{2 \pi}{N_x \Delta x}
\left[ \frac{q_h}{N_y}\right], \hspace{0.25in} {\rm and}$](img58.png)
![$\displaystyle \Delta k_y q_y = \frac{2 \pi}{N_y \Delta y}
\left(
q_h - N_y \left[ \frac{q_h}{N_y}\right]
\right)$](img60.png)