PROOF FOR A 1-D EARTH

Next: SYNTHETIC DATA Up: CONJECTURE Previous: CONJECTURE

PROOF FOR A 1-D EARTH

The proof of this conjecture for a one dimensional earth is given as a problem set in Claerbout (1976). The outline of the derivation that follows uses the transform approach developed there, where is the unit delay operator $e^{-i\omega \Delta t}$ .

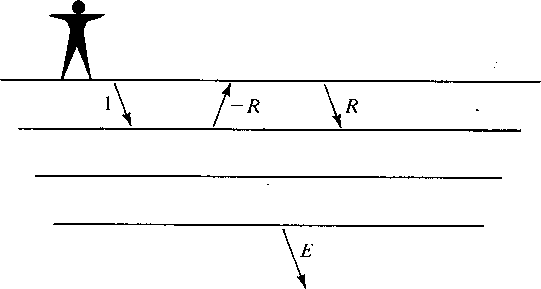
Consider a plane-layered Earth model with the reflection seismology geometry shown in Figure 1. If the system is lossless then the energy flux through the top layer has to be equal to the flux through the half-space below. Therefore,

$\begin{displaymath} Y_1 \left\{ R\left(\frac{1}{Z}\right) R(Z) - \left[1+R\left... ...ight] [1+R(Z)] \right\} = - Y_k E\left(\frac{1}{Z}\right) E(Z) \end{displaymath}$

(1)

where

is the impedance of the top layer and

is the impedance of the half-space, or

$\begin{displaymath} 1 + R\left(\frac{1}{Z}\right) + R(Z) = \frac{Y_k}{Y_1} E\left(\frac{1}{Z}\right) E(Z) \end{displaymath}$

(2)

8-7 Figure 1. Reflection seismology geometry - Claerbout (1979).

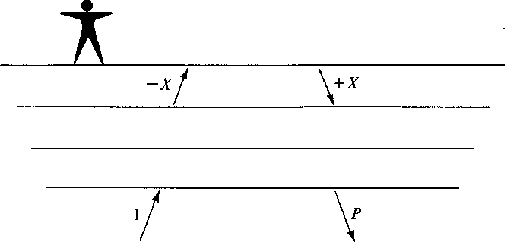
Comparing the reflection seismology geometry with the earthquake seismology geometry shown in Figure 2 gives by reciprocity. Therefore

$\begin{displaymath} 1 + R\left(\frac{1}{Z}\right) + R(Z) = (constant) \; X\left(\frac{1}{Z}\right) X(Z) \end{displaymath}$

(3)

Since

for times less than zero, this means the positive time part of the `earthquake' seismogram's auto-correlation function equals the reflection seismogram.

This theorem can be extended to a two dimensional plane-layered Earth by considering slant stacks (Claerbout, 1985).

8-8 Figure 2. Earthquake seismology geometry - from Claerbout (1979). All the waves (1, and ) could be multiplied by the same random signal, and this would not effect their spectra or auto-correlation functions.

Next: SYNTHETIC DATA Up: CONJECTURE Previous: CONJECTURE

2015-03-23