 |
 |
 |
 | Velocity analysis using similarity-weighted semblance |  |
![[pdf]](icons/pdf.png) |
Next: Review of local similarity
Up: Theory
Previous: Traditional semblance
The semblance can be thought as a squared correlation between the analyzed signal and a weighting function 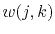 in the following form:
in the following form:
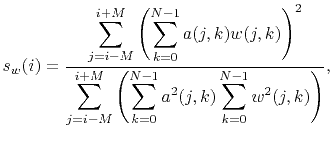 |
(2) |
where 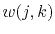 denotes the weighting function for time index
denotes the weighting function for time index 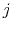 and trace number
and trace number 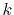 .
.
With 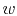 selected using different criterion, equation 2 can lead to different well-known semblance types:
selected using different criterion, equation 2 can lead to different well-known semblance types:
- When
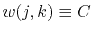 , where
, where 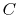 is a constant, equation 2 turns to the traditional semblance 1.
is a constant, equation 2 turns to the traditional semblance 1.
- When
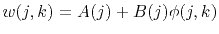 , where
, where 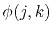 is a known function,
is a known function, 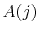 and
and 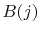 are two coefficients estimated from the least-squares fitting for the trend function
are two coefficients estimated from the least-squares fitting for the trend function 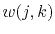 , equation 2 turns to the AB semblance proposed by Fomel (2009). The AB semblance is proposed to handle the velocity analysis for those CMP gathers with AVO phenomenon. Appendix A provides a short review of calculating
, equation 2 turns to the AB semblance proposed by Fomel (2009). The AB semblance is proposed to handle the velocity analysis for those CMP gathers with AVO phenomenon. Appendix A provides a short review of calculating 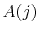 and
and 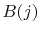 in the AB semblance.
in the AB semblance.
More recently, Luo and Hale (2012) proposed another weighting approach which honors the large-offset data and damping the small-offset data to increase the resolution for the resulted velocity scanning map.
In this abstract, we propose to use local similarity (Fomel, 2007) to weight different traces:
![$\displaystyle w(j,k)=\mathcal{\mathbf{S}}[a(j,k),r(j)],$](img24.png) |
(3) |
where
![$ \mathcal{\mathbf{S}}[\mathbf{x},\mathbf{y}]$](img25.png) denotes the local similarity between traces
denotes the local similarity between traces
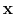 and
and
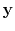 ,
, 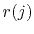 denotes the
denotes the 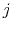 th time point for a selected reference trace
th time point for a selected reference trace
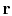 . The reference can be easily selected as the zero-offset trace, or more plausible, as the stacked trace using the conventional stacking technique or a more sophisticated stacking technique (Liu et al., 2009). In most cases, when the signal-to-noise ratio (SNR) of the CMP gather is not low, the choice of reference trace will not affect the performance too much. However, when the CMP gather is very noisy, the stacked trace using a better stacking technique can help obtain a better focused and smoother semblance map.
. The reference can be easily selected as the zero-offset trace, or more plausible, as the stacked trace using the conventional stacking technique or a more sophisticated stacking technique (Liu et al., 2009). In most cases, when the signal-to-noise ratio (SNR) of the CMP gather is not low, the choice of reference trace will not affect the performance too much. However, when the CMP gather is very noisy, the stacked trace using a better stacking technique can help obtain a better focused and smoother semblance map.
Figure 1 gives a brief demonstration of the proposed similarity-weighted semblance. Figure 1a is a simple NMO corrected CMP gather with some Gaussian white noise. There are two abnormal traces in the gather. For traditional semblance, the two abnormal traces are given equal weights, which is not plausible. Figure 1b shows the weights applied to each trace for the semblance calculation. The weights equal to the local similarity between each trace and the stacked trace.
As we can see from the map of weights, the two abnormal traces are given much low weights. The more reasonable semblance calculation will result in a much higher resolution, which will be exclusively demonstrated in the section of examples. In the next section, we will give a brief review of the theory of local similarity.
 |
 |
 |
 | Velocity analysis using similarity-weighted semblance |  |
![[pdf]](icons/pdf.png) |
Next: Review of local similarity
Up: Theory
Previous: Traditional semblance
2015-06-25
![]() selected using different criterion, equation 2 can lead to different well-known semblance types:
selected using different criterion, equation 2 can lead to different well-known semblance types: