Next: GARDNER'S SMEAR OPERATOR
Up: ROCCA'S SMEAR OPERATOR
Previous: Push and pull
It is worth noticing that the concepts in this section
are not limited to constant velocity
but apply as well to  .
However,
the circle operator
.
However,
the circle operator  presents some difficulties.
Let us see why.
Starting from the Dix moveout approximation,
presents some difficulties.
Let us see why.
Starting from the Dix moveout approximation,
 ,
we can directly solve for
,
we can directly solve for  but finding
but finding 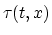 is an iterative process at best.
Even worse, at wide offsets, hyperbolas cross one another
which means that
is an iterative process at best.
Even worse, at wide offsets, hyperbolas cross one another
which means that 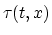 is multivalued.
The spray (push)
operators
is multivalued.
The spray (push)
operators  and
and  loop over inputs
and compute the location of their outputs.
Thus
loop over inputs
and compute the location of their outputs.
Thus
 requires we compute
requires we compute  from
from  so it is
one of the troublesome cases.
Likewise, the sum (pull)
operators
so it is
one of the troublesome cases.
Likewise, the sum (pull)
operators  and
and  loop over outputs.
Thus
loop over outputs.
Thus
 causes us the same trouble.
In both cases, the circle operator
turns out to be the troublesome one.
As a consequence, most practical work is done with
the hyperbola operator.
causes us the same trouble.
In both cases, the circle operator
turns out to be the troublesome one.
As a consequence, most practical work is done with
the hyperbola operator.
A summary of the meaning of the Rocca smile
and its adjoint is found in Figures
8.21 and 8.22.

|
|---|
yalei2
Figure 21.
Impulses on a zero-offset section migrate
to semicircles.
The corresponding constant-offset section
contains the adjoint of the Rocca smile.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|

|
|---|
yalei1
Figure 22.
Impulses on a constant-offset section
become ellipses in depth and
Rocca smiles on the zero-offset section.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
Next: GARDNER'S SMEAR OPERATOR
Up: ROCCA'S SMEAR OPERATOR
Previous: Push and pull
2009-03-16

