Moveout, velocity, and stacking

VELOCITY SPECTRA

An important transformation in exploration geophysics takes data as a function of shot-receiver offset and transforms it to data as a function of apparent velocity. Data is summed along hyperbolas of many velocities. This important industrial process is adjoint to another that may be easier to grasp: data is synthesized by a superposition of many hyperbolas. The hyperbolas have various asymptotes (velocities) and various tops (apexes). Pseudocode for these transformations is

		do $v$ {  


do $\tau$ { 


do $x$ {

$t = \sqrt{ \tau^2 + x^2/v^2 }$ 


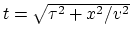
if hyperbola superposition 


data$(t,x)$ = data$(t,x)$ + vspace$(\tau,v)$ 


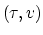
else if velocity analysis 


vspace$(\tau,v)$ = vspace$(\tau,v)$ + data$(t,x)$

}}}

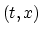
This pseudocode transforms one plane to another using the equation $t^2 = \tau^2 +x^2/v^2$. This equation relates four variables, the two coordinates of the data space $(t,x)$ and the two of the model space $(\tau,v)$. Suppose a model space is all zeros except for an impulse at $(\tau_0, v_0)$. The code copies this inpulse to data space everywhere where $t^2 = \tau_0^2 + x^2/v_0^2$. In other words, the impulse in velocity space is copied to a hyperbola in data space. In the opposite case an impulse at a point in data space $(t_0,x_0)$ is copied to model space everywhere that satisfies the equation $t_0^2 = \tau^2 + x_0^2/v^2$. Changing from velocity space to slowness space this equation $t_0^2 = \tau^2 + x_0^2 s^2$ has a name. In $(\tau, s)$-space it is an ellipse (which reduces to a circle when $x_0^2=1$.

Look carefully in the model spaces of Figure 4.7 and Figure 4.8. Can you detect any ellipses? For each ellipse, does it come from a large $x_0$ or a small one? Can you identify the point $(t_0,x_0)$ causing the ellipse?

We can ask the question, if we transform data to velocity space, and then return to data space, will we get the original data? Likewise we could begin from the velocity space, synthesize some data, and return to velocity space. Would we come back to where we started? The answer is yes, in some degree. Mathematically, the question amounts to this: Given the operator $\bold A$, is $\bold A'\bold A$ approximately an identity operator, i.e. is $\bold A$ nearly a unitary operator? It happens that $\bold A'\bold A$ defined by the pseudocode above is rather far from an identity transformation, but we can bring it much closer by including some simple scaling factors. It would be a lengthy digression here to derive all these weighting factors but let us briefly see the motivation for them. One weight arises because waves lose amplitude as they spread out. Another weight arises because some angle-dependent effects should be taken into account. A third weight arises because in creating a velocity space, the near offsets are less important than the wide offsets and we do not even need the zero-offset data. A fourth weight is a frequency dependent one which is explained in chapter . Basically, the summations in the velocity transformation are like integrations, thus they tend to boost low frequencies. This could be compensated by scaling in the frequency domain with frequency as $\sqrt{-i\omega}$. with subroutine halfint() .

The weighting issue will be examined in more detail later. Meanwhile, we can see nice quality examples from very simple programs if we include the weights in the physical domain, $w= \sqrt{1/t}\; \sqrt{x/v}\; \tau /t$. (Typographical note: Do not confuse the weight $w$ (double you) with omega $\omega$.) To avoid the coding clutter of the frequency domain weighting $\sqrt{-i\omega}$ I omit that, thus getting smoother results than theoretically preferable. Figure 4.7 illustrates this smoothing by starting from points in velocity space, transforming to offset, and then back and forth again.

velvel
Figure 7. Iteration between spaces. Left are model spaces. Right are data spaces. Right derived from left. Lower model space derived from upper data space.

There is one final complication relating to weighting. The most symmetrical approach is to put $w$ into both $\bold A$ and $\bold A'$. Thus, because of the weighting by $\sqrt{x}$, the synthetic data in Figure 4.7 is nonphysical. An alternate view is to define $\bold A$ (by the pseudo code above, or by some modeling theory) and then for reverse transformation use $w^2\bold A'$.

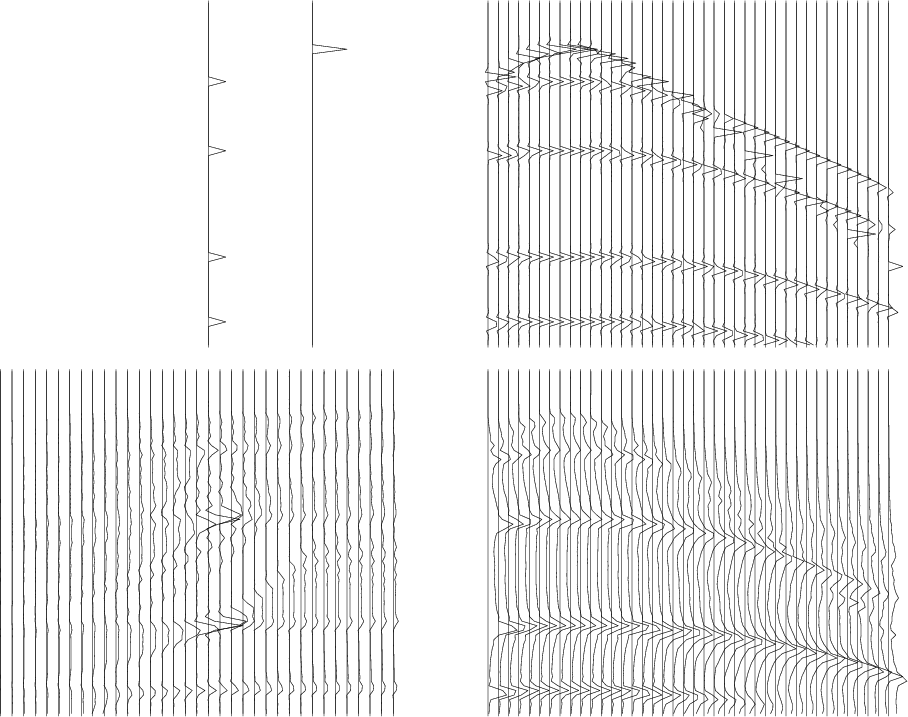
An example is shown in Figure 4.8.

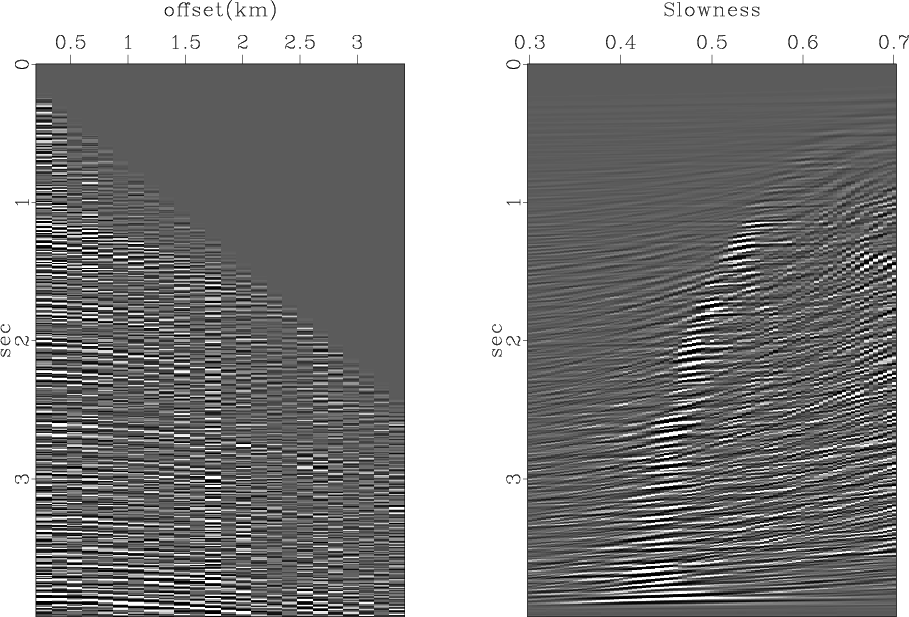
mutvel
Figure 8. Transformation of data as a function of offset (left) to data as a function of slowness (velocity scans) on the right using subroutine velsimp().

Moveout, velocity, and stacking