Time-shift imaging condition in seismic migration

Space-shift imaging condition

A generalized prestack imaging condition (Sava and Fomel, 2005) estimates image reflectivity using cross-correlation in space and time, followed by image extraction at zero time:

$$U \left ({ \bf m},{ \bf h}, t \right ) = U_r \left ({ \bf m}+{ \bf h}, t \right )\ast U_s \left ({ \bf m}-{ \bf h}, t \right )\;,$$ (3)

$$R \left ({ \bf m},{ \bf h}\right ) = U \left ({ \bf m},{ \bf h},t=0 \right )\;.$$ (4)

Here, ${ \bf h}= \left[ h_x,h_y,h_z \right]$ is a vector describing the space-shift between the source and receiver wavefields prior to imaging. Special cases of this imaging condition are horizontal space-shift (Rickett and Sava, 2002) and vertical space-shift (Biondi and Symes, 2004).

For computational reasons, this imaging condition is usually implemented in the Fourier domain using the expression

$$R \left ({ \bf m},{ \bf h}\right )= \sum_\omega U_r \left... ...ga \right ) U_s^* \left ({ \bf m}-{ \bf h},\omega \right )\;.$$ (5)

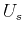The $^*$ sign represents a complex conjugate applied on the receiver wavefield $U_s$ in the Fourier domain.

Time-shift imaging condition in seismic migration