Elastic wave-mode separation for TTI media

Wave-mode separation for 3D TI media

In order to separate all three modes--P, SV, and SH--in a 3D TI medium, one needs to construct 3D separators. Dellinger (1991) shows that P-waves can be separated from two shear modes by a straightforward extension of the 2D algorithm. Indeed, for 3D TI media, one can always obtain the P-mode by constructing P-wave separators represented by the polarization vector $W_P=\{U_x, U_y, U_z \}$ and then projecting the 3D elastic wavefields onto the vector $W_P$ . The P-wave polarization vector with components $\{U_x, U_y, U_z\}$ is obtained by solving the 3D Christoffel matrix (Aki and Richards, 2002; Tsvankin, 2005):

$$\left [ \mtrx{ G_{11}-\rho V^2 & G_{12} & G_{13}\ G_{12} & G_{22... ...23} & G_{33} -\rho V^2 } \right] \left [\mtrx{ U_x\ U_y\ U_z} \right] =0 .$$ (13)

The notations in this equation have the same definitions as in equation 2. For TTI media, the matrix ${\mathbf G}$ has the elements

$$G_{11} = c_{11}n_x^2+c_{66}n_y^2+c_{55}n_z^2 +2 c_{16}n_xn_y+2 c_{15}n_xn_z+2c_{56}n_yn_z ,$$ (14)

$$G_{22} = c_{66}n_x^2+c_{22}n_y^2+c_{44}n_z^2 +2 c_{26}n_xn_y+ (c_{45}+c_{46})n_xn_z+2c_{24}n_yn_z ,$$ (15)

$$G_{33} = c_{55}n_x^2+c_{44}n_y^2+c_{33}n_z^2 +2 c_{45}n_xn_y+2 c_{35}n_xn_z+2c_{34}n_yn_z ,$$ (16)

$$G_{12} = c_{16}n_x^2+c_{26}n_y^2+c_{45}n_z^2 + (c_{12}+c_{66})n_xn_y+ (c_{14}+c_{56})n_xn_z+(c_{25}+c_{46})n_yn_z ,$$ (17)

$$G_{13} = c_{15}n_x^2+c_{46}n_y^2+c_{35}n_z^2 + (c_{14}+c_{56})n_xn_y+ (c_{13}+c_{55})n_xn_z+(c_{36}+c_{45})n_yn_z ,$$ (18)

$$G_{23} = c_{56}n_x^2+c_{24}n_y^2+c_{34}n_z^2 + (c_{25}+c_{46})n_xn_y+ (c_{36}+c_{45})n_xn_z+(c_{23}+c_{44})n_yn_z .$$

When constructing shear mode separators, one faces an additional complication: SV- and SH-waves have the same velocity along the symmetry axis of a 3D TI medium, and this singularity prevents one from obtaining polarization vectors for shear modes in this particular direction by solving the Christoffel equation (Tsvankin, 2005). In 3D TI media, the polarization of the shear modes around the singular directions are non-linear and cannot be characterized by a plane-wave solution. Consequently, constructing 3D global separators for fast and slow shear modes is difficult.

To mitigate the effects of the shear wave-mode singularity, I use the mutual orthogonality among the P, SV, and SH modes depicted in Figure 6. In this figure, vector ${\bf n}=\{\sin\nu\cos\alpha,\sin\nu\sin\alpha,\cos\nu\}$ represents the symmetry axis of a TTI medium, with $\nu$ and $\alpha$ being the tilt and azimuth of the symmetry axis, respectively. The wave vector ${\bf k}$ characterizes the propagation direction of a plane wave. Vectors ${\mathbf P}$ , ${\mathbf {SV}}$ , and ${\mathbf {SH}}$ symbolize the compressional, and fast and slow shear polarization directions, respectively. For TI media, plane waves propagate in symmetry planes, and the symmetry axis ${\bf n}$ and any wave vector ${\bf k}$ form a symmetry plane. For a plane wave propagating in the direction ${\bf k}$ , the P-wave is polarized in this symmetry plane and deviates from the vector ${\bf k}$ ; the SV- and SH-waves are polarized perpendicular to the P-mode, in and out of the symmetry plane, respectively.

Using this mutual orthogonality among all three modes, I first obtain the SH-wave polarization vector $W_{SH}$ by cross multiplying vectors ${\bf n}$ and ${\bf k}$ , which ensures that the SH mode is polarized orthogonal to symmetry planes:

$$W_{SH} = {\bf n}\times{\bf k}$$

$$= \{ k_z n_y-k_y n_z,$$

$$k_x n_z- k_z n_x,$$

$$k_y n_x - k_x n_y \} .$$ (19)

Then I calculate the SV polarization vector $W_{SV}$ by cross multiplying polarization vectors P and SH modes, which ensures the orthogonality between SV and P modes and SV and SH modes:

$$W_{SV} = W_{P}\times W_{SH} ,$$

$$= \{ k_y n_x U_y - k_x n_y U_y+k_z n_x U_z - k_x n_z U_z,$$

$$k_z n_y U_z - k_y n_z U_z+k_x n_y U_x - k_y n_x U_x,$$

$$k_x n_z U_x - k_z n_x U_x+k_y n_z U_y - k_z n_y U_y \} .$$ (20)

Here, the magnitude of the P-wave polarization vectors for a certain wavenumber $\vert{\bf k}\vert$ is a constant:

$$\left\vert U_{P} \right\vert = \sqrt{U_x^2+U_y^2+U_z^2}=c .$$ (21)

This ensures that for a certain wavenumber, P-waves obtained by projecting the elastic wavefields onto the polarization vectors are uniformly scaled. For comparison, the magnitudes of all three modes are respectively

$$\left\vert U_{P} \right\vert = c ,$$ (22)

$$\left\vert U_{SV}\right\vert = c\sin\phi ,$$ (23)

$$\left\vert U_{SH}\right\vert = c\sin\phi ,$$ (24)

where $\phi$ is the polar angle of the propagating plane wave, i.e., the angle between vectors ${\bf k}$ and ${\bf n}$ . Figure 7 shows the polarization vectors of P-, SH-, and SV-modes computed using equations 13, 20, and 21, respectively. The P-wave polarization vectors in Figure 7(a) all have the same magnitude, but the SV and SH polarization vectors in Figures 7(c) and fig:polar3dS2 vary in magnitude. In the symmetry axis direction, they become zero. The zero amplitude of the shear modes in the symmetry axis direction is not an abrupt but a continuous change over nearby propagation angles. Using separators represented by solutions to equation 13 and expressions 20 and 21 to filter the wavefields, I obtain separated shear modes that are scaled differently than the P-mode. For a certain wavenumber, the shear modes are scaled by $\sin\phi$ , with $\phi$ being the polar angle, which increases from zero in the symmetry axis to unity in the orthogonal propagation directions. Therefore, the separated SV- and SH-waves have zero amplitude in the symmetry axis direction, and the amplitudes of the shear modes are just kinematically correct.

The components of the polarization vectors for P-, SV-, and SH-waves can be transformed back to the space domain to construct spatial filters for 3D heterogeneous TI media. For example, Figure 8 illustrates nine spatial filters transformed from the Cartesian components of the polarization vectors shown in Figure 7. All these filters can be spatially varying when the medium is heterogeneous. Therefore, in principle, wave-mode separation in 3D would perform well even for models that have complex structures and arbitrary tilts and azimuths of TI symmetry.

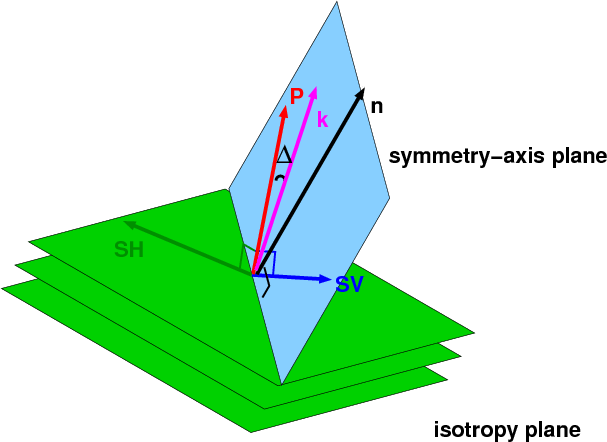
polar3d
Figure 6. A schematic showing the elastic wave-modes polarization in a 3D TI medium. The three parallel planes represent the isotropy planes of the medium. The vector ${\bf n}$ represents the symmetry axis, which is orthogonal to the isotropy plane. The vector ${\bf k}$ is the propagation direction of a plane wave. The wave-modes P, SV, and SH are polarized in the direction ${\mathbf P}$ , ${\mathbf {SV}}$ , and ${\mathbf {SH}}$ , respectively. The three modes are polarized orthogonal to each other.

polar3dP,polar3dS2,polar3dS1
Figure 7. The wave-mode polarization for P-, SH-, and SV-mode for a VTI medium with parameters $V_{P0}=4.95$  km/s, $V_{S0}=2.48$  km/s, $\epsilon=0.4$ , and $\delta=0.1$ . The P-mode polarization is computed using the 3D Christoffel equation, and SV and SH polarizations are computed using Equations 21 and 20. Note that the SV- and SH-wave polarization vectors have zero amplitude in the vertical direction.

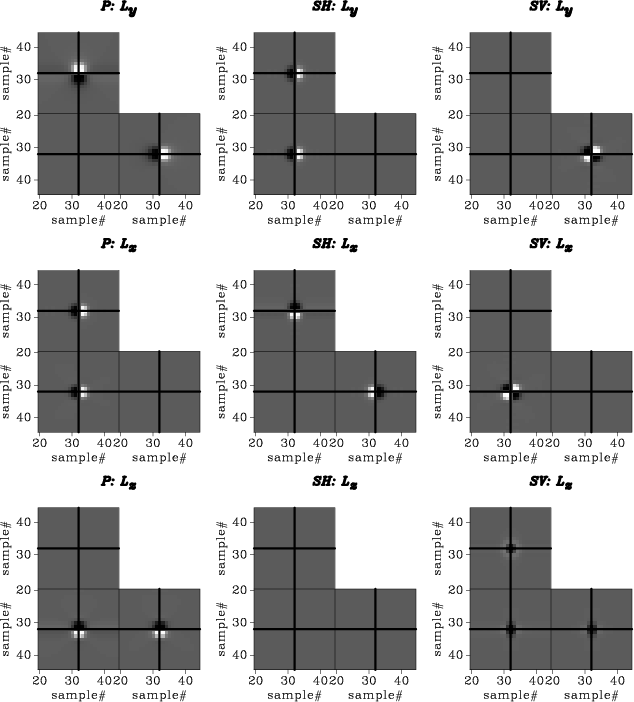
filters3d
Figure 8. The separation filters $L_x$ , $L_y$ , and $L_z$ for the P, SV, and SH modes for a VTI medium. The corresponding wavenumber-domain polarization vectors are shown in Figure 7. Note that the filter $L_z$ for the SH mode is blank because the $z$ component of the polarization vector is zero. The zoomed views show $24\times 24$ samples out of the original $64\times 64$ samples around the center of the filters.

Elastic wave-mode separation for TTI media