 |
 |
 |
 | Multidimensional autoregression |  |
![[pdf]](icons/pdf.png) |
Next: Seabeam: theory to practice
Up: LEVELED INVERSE INTERPOLATION
Previous: Test results for leveled
Here we see how the interpolation beyond aliasing was done.
The first ``statement of wishes'' is that the observational data  should result from a linear interpolation
should result from a linear interpolation  of the uniformly sampled
model space
of the uniformly sampled
model space  ; that is,
; that is,
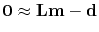 .
Expressing this as a change
.
Expressing this as a change
 gives the fitting goal
in terms of the model change,
gives the fitting goal
in terms of the model change,
 .
The second wish is really an assertion
that a good way to find missing parts of a function
(the model space)
is to solve for the function and its PEF at the same time.
We are merging the fitting goal
(
.
The second wish is really an assertion
that a good way to find missing parts of a function
(the model space)
is to solve for the function and its PEF at the same time.
We are merging the fitting goal
(![[*]](icons/crossref.png) ) for irregularly sampled data with the fitting goal
(44) for finding the prediction-error filter.
) for irregularly sampled data with the fitting goal
(44) for finding the prediction-error filter.
Writing this out in full for 3 data points
and 6 model values on a uniform mesh
and a PEF of 3 terms,
we have
![$\displaystyle \left[ \begin{array}{cccccc\vert ccc} .8 & .2 & . & . & . & . & &...
..._{m4} \ r_{m5} \ r_{m6} \ r_{m7} \end{array} \right] \quad \approx \bold 0$](img215.png) |
(52) |
where  is the convolution of the filter
is the convolution of the filter 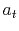 and the model
and the model  ,
where
,
where  is the data misfit
is the data misfit
 ,
and where
,
and where  was defined in equation (11).
was defined in equation (11).
Before you begin to use this nonlinear fitting goal,
you need some starting guesses for  and
and  .
The guess
.
The guess
 is satisfactory (as explained later).
For the first guess of the filter, I suggest you load it up with
is satisfactory (as explained later).
For the first guess of the filter, I suggest you load it up with
 as I did for the examples here.
as I did for the examples here.
 |
 |
 |
 | Multidimensional autoregression |  |
![[pdf]](icons/pdf.png) |
Next: Seabeam: theory to practice
Up: LEVELED INVERSE INTERPOLATION
Previous: Test results for leveled
2013-07-26
![]() and
and ![]() .
The guess
.
The guess
![]() is satisfactory (as explained later).
For the first guess of the filter, I suggest you load it up with
is satisfactory (as explained later).
For the first guess of the filter, I suggest you load it up with
![]() as I did for the examples here.
as I did for the examples here.