|
|
|
|
Homework 4 |
Using the theory of geometric integration, show that ![]() will contain a geometric event
will contain a geometric event
![]() .
Find
.
Find ![]() and
and ![]() .
.
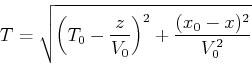 |
(6) |
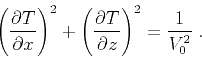 |
(7) |
Suppose that you switch to the more accurate shifted-hyperbola approximation
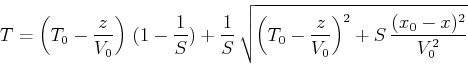 |
(8) |
 |
(9) | ||
 |
(10) |
|
|
|
|
Homework 4 |