Next: Bibliography Up: Liu et al.: VD-seislet Previous: Acknowledgments

Appendix: The lifting scheme for DWT

The lifting scheme (Sweldens, 1995) provides a convenient approach for defining wavelet transforms by breaking them down into the following steps:

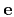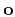Divide data into even and odd components, $\mathbf{e}$ and $\mathbf{o}$ .
Find a residual difference, 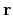$\mathbf{r}$ , between the odd component and its prediction from the even component:

$\begin{displaymath} \mathbf{r} = \mathbf{o} - \mathbf{P[e]}\;, \end{displaymath}$ (20)

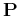where $\mathbf{P}$ is a prediction operator.
Find a coarse approximation, 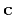$\mathbf{c}$ , of the data by updating the even component:

$\begin{displaymath} \mathbf{c} = \mathbf{e} + \mathbf{U[r]}\;, \end{displaymath}$ (21)

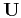where $\mathbf{U}$ is an update operator.
The coarse approximation, 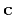$\mathbf{c}$ , becomes the new data, and the sequence of steps is repeated at the next scale.

The Cohen-Daubechies-Feauveau (CDF) 5/3 biorthogonal wavelets (Cohen et al., 1992) are constructed by making the prediction operator a linear interpolation between two neighboring samples,

$\begin{displaymath} \mathbf{P[e]}_k = \left(\mathbf{e}_{k-1} + \mathbf{e}_{k}\right)/2\;, \end{displaymath}$

(22)

and by constructing the update operator to preserve the running average of the signal (Sweldens and Schröder, 1996), as follows:

$\begin{displaymath} \mathbf{U[r]}_k = \left(\mathbf{r}_{k-1} + \mathbf{r}_{k}\right)/4\;. \end{displaymath}$

(23)

Furthermore, one can create a high-order CDF 9/7 biorthogonal wavelet transform by using CDF 5/3 biorthogonal wavelets twice with different lifting operator coefficients (Lian et al., 2001). The transform is easily inverted according to reversing the steps above:

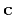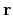Start with the coarsest scale data representation $\mathbf{c}$ and the coarsest scale residual $\mathbf{r}$ .
Reconstruct the even component 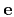$\mathbf{e}$ by reversing the operation in equation A-2, as follows:

$\begin{displaymath} \mathbf{e} = \mathbf{c} - \mathbf{U[r]}\;, \end{displaymath}$ (24)
Reconstruct the odd component 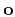$\mathbf{o}$ by reversing the operation in equation A-1, as follows:

$\begin{displaymath} \mathbf{o} = \mathbf{r} + \mathbf{P[e]}\;, \end{displaymath}$ (25)
Combine the odd and even components to generate the data at the previous scale level and repeat the sequence of steps.

Next: Bibliography Up: Liu et al.: VD-seislet Previous: Acknowledgments

2015-10-24