Test case for PEF estimation with sparse data II

The Test Case

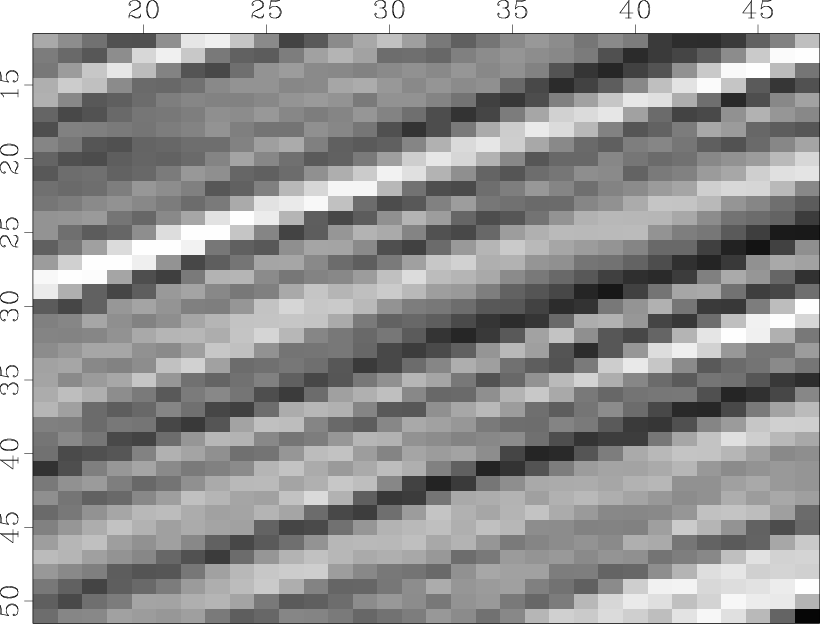
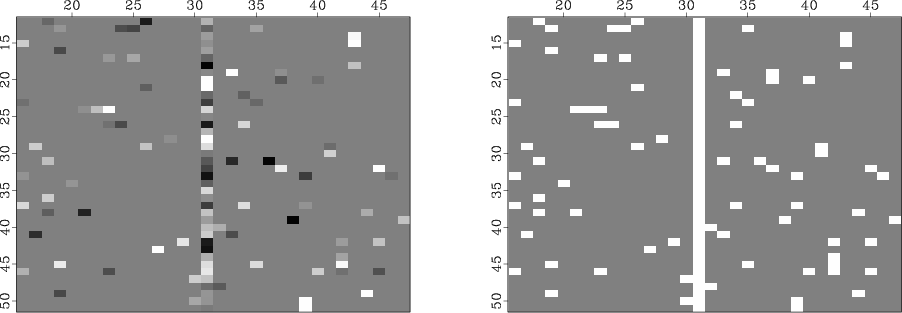
Claerbout (2000) proposes a test case for which the Gaussian curvature of the model vanishes. In this paper, we present an even simpler test case. Given a 2-D random field, we deconvolve with a known dip (or steering) (Clapp et al., 1997) filter to obtain a ``plane wave'' model, as shown in Figure 1. To simulate collected ``data'', we sampled the model of Figure 1 at about 60 points randomly, and about two-thirds of the way down one trace in the center. The results are shown in Figure 2.

model Figure 1. True model - plane waves dipping at $22.5^{\circ }$.

data
Figure 2. Left: Collected data - one known trace, about 60 randomly-selected known data points. Right: Known data selector.

Test case for PEF estimation with sparse data II