Predictive painting spreads information from a seed trace to its neighbors recursively by following the local dip (Fomel, 2010).
The spreading or “painting” process can be implemented using plane-wave construction filter (Fomel and Guitton, 2006).
The mathematical basis of this filter is a differential equation for local plane waves (Claerbout, 1992),
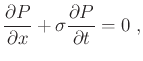 |
(1) |
where 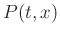 is the wavefield and
is the wavefield and 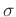 is the local slope.
In the case of a constant slope, equation 1 has the simple general solution
is the local slope.
In the case of a constant slope, equation 1 has the simple general solution
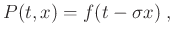 |
(2) |
where 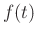 is an arbitrary waveform.
Equation 2 is nothing more than a mathematical description of a plane wave.
Assuming that the slope
is an arbitrary waveform.
Equation 2 is nothing more than a mathematical description of a plane wave.
Assuming that the slope
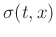 varies in time and space, we can design a local operator to propagate trace
varies in time and space, we can design a local operator to propagate trace
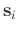 to trace
to trace
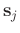 , and describe such prediction as
, and describe such prediction as
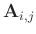 .
If
.
If
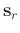 is a reference trace, spreading its information to a distant neighbor
is a reference trace, spreading its information to a distant neighbor
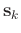 (for example
(for example 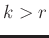 ) can be accomplished by simple recursion:
) can be accomplished by simple recursion:
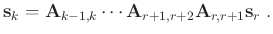 |
(3) |
The recursive operator in Equation 3 is referred to as predictive painting (Fomel, 2010).
2019-05-06