Next: Definition of local correlation
Up: Measuring local similarity
Previous: Measuring local similarity
Global correlation coefficient between  and
and  can be
defined as the functional
can be
defined as the functional
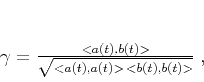 |
(8) |
where 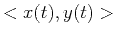 denotes the dot product between two signals:
denotes the dot product between two signals:
According to definition 8, the correlation
coefficient of two identical signals is equal to one, and the
correlation of two signals with opposite polarity is minus one. In all
the other cases, the correlation will be less then one in magnitude
thanks to the Cauchy-Schwartz inequality.
The global measure 8 is inconvenient because it
supplies only one number for the whole signal. The goal of local
analysis is to turn the functional into an operator and to produce
local correlation as a variable function 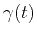 that identifies
local changes in the signal similarity.
that identifies
local changes in the signal similarity.
2013-07-26
![]() and
and ![]() can be
defined as the functional
can be
defined as the functional
![]() that identifies
local changes in the signal similarity.
that identifies
local changes in the signal similarity.