|
|
|
|
De-aliased seismic data interpolation using seislet transform with low-frequency constraint |
Next: Conclusion Up: De-aliased seismic data interpolation Previous: De-aliased interpolation by low-frequency
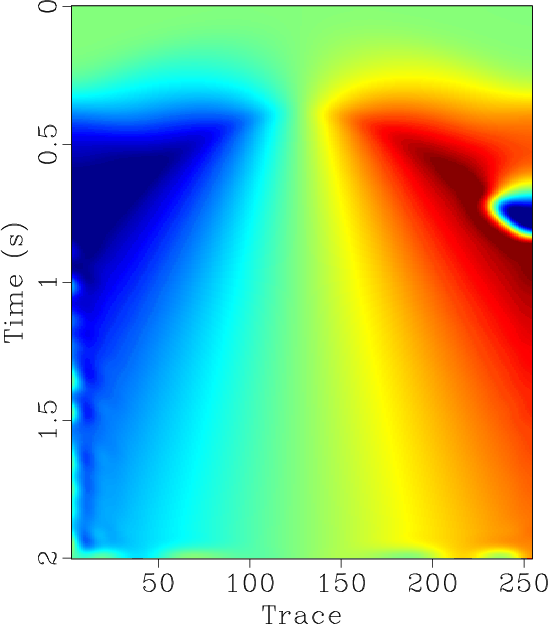
As we can see, the spectrum of the reconstructed data using the proposed approach is exactly the same as the original data. If we use a filter with a somewhat higher low-pass frequency, we will obtain a much worse reconstructed result, because of the severe aliasing problem. Figure 6a shows the precise dip estimation from the original data. Figure 6b shows the final dip estimation using 15 Hz low-pass filtering. The final dip estimation using 30 Hz low-pass filtering shows incorrect dips around 0.75 s at trace 250 (Figure 6c).
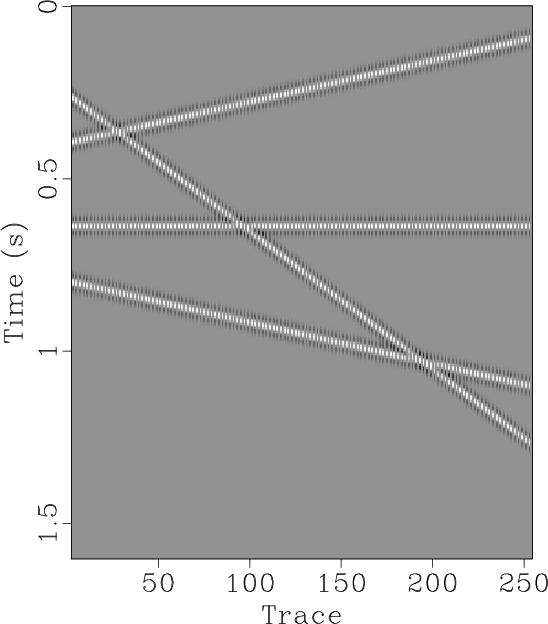
The second synthetic example is a linear-event example to test the performance of the proposed approach on post-stack data. The original data is shown in Figure 8a. We also remove 50% traces regularly. In this example, we compare the proposed approach with the ![]() based POCS approach. The reconstructed results using the proposed approach and the
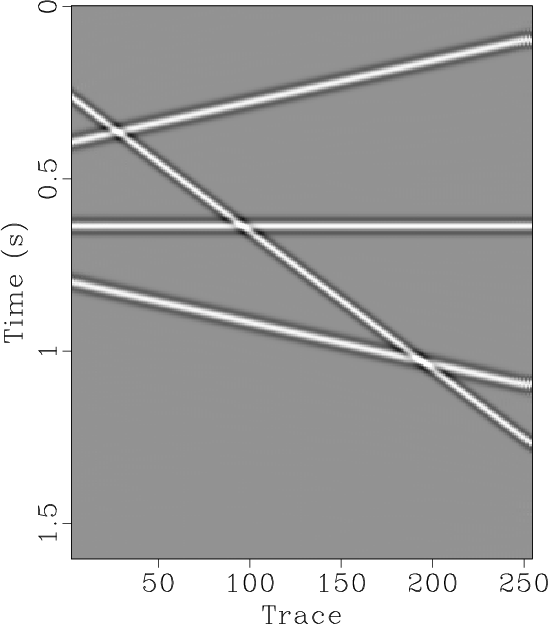
based POCS approach. The reconstructed results using the proposed approach and the ![]() based POCS approach are shown in Figures 8c and 8d, respectively. It is obvious that the proposed can still obtain a perfect performance, while the
based POCS approach are shown in Figures 8c and 8d, respectively. It is obvious that the proposed can still obtain a perfect performance, while the ![]() based POCS approach cannot obtain any improvement because of the strong aliasing noise in the
based POCS approach cannot obtain any improvement because of the strong aliasing noise in the ![]() domain. This test confirms the fact that
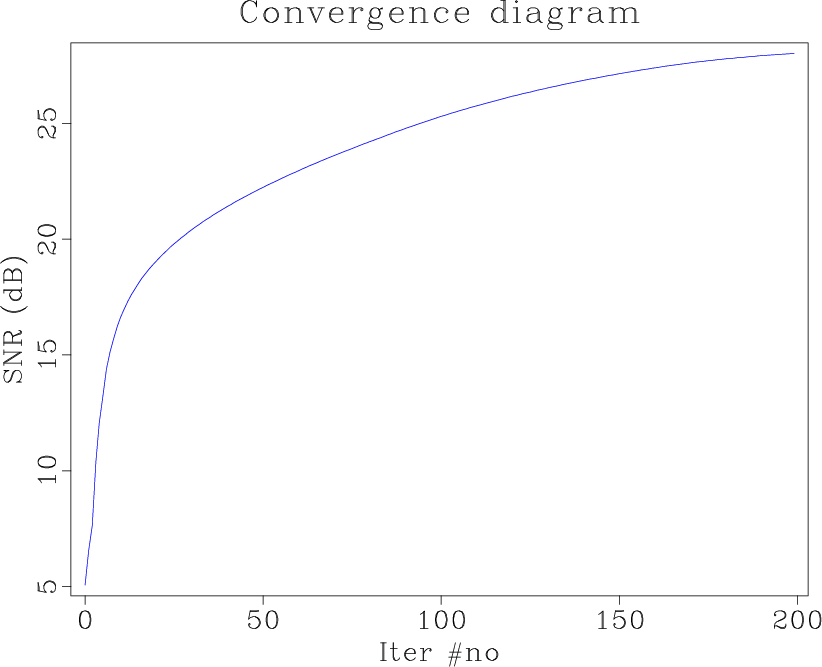
domain. This test confirms the fact that ![]() based POCS approach should not be used to interpolate regularly missing traces Spitz (1991); Naghizadeh and Sacchi (2007,2010). In this example, we use 100 iterations to obtain the reconstructed results of both seislet and Fourier transforms. The final SNR of the proposed approach reaches 22.47 dB, and the SNR of the
based POCS approach should not be used to interpolate regularly missing traces Spitz (1991); Naghizadeh and Sacchi (2007,2010). In this example, we use 100 iterations to obtain the reconstructed results of both seislet and Fourier transforms. The final SNR of the proposed approach reaches 22.47 dB, and the SNR of the ![]() based POCS approach stays unchanged: 3.007 dB. The slightly worse performance of the proposed approach on this example than the first example is because the crossing seismic events cause some errors when estimating the local slope, which affect the final performance a bit.
based POCS approach stays unchanged: 3.007 dB. The slightly worse performance of the proposed approach on this example than the first example is because the crossing seismic events cause some errors when estimating the local slope, which affect the final performance a bit.



|
|---|
|
hyper,hyper-zero,fk-hyper,fk-hyper-zero
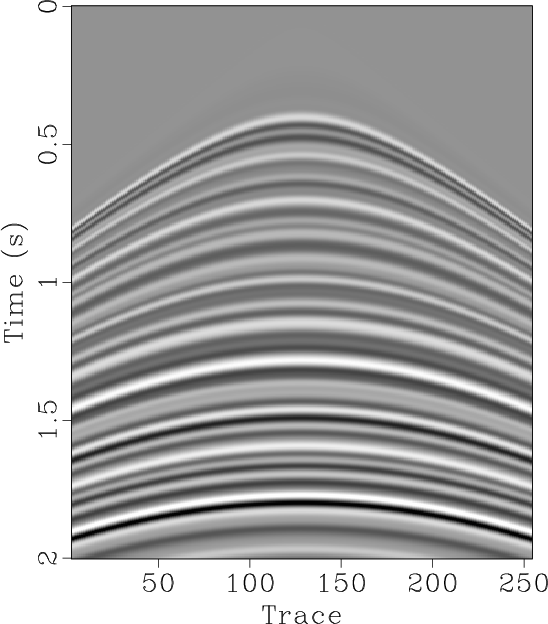
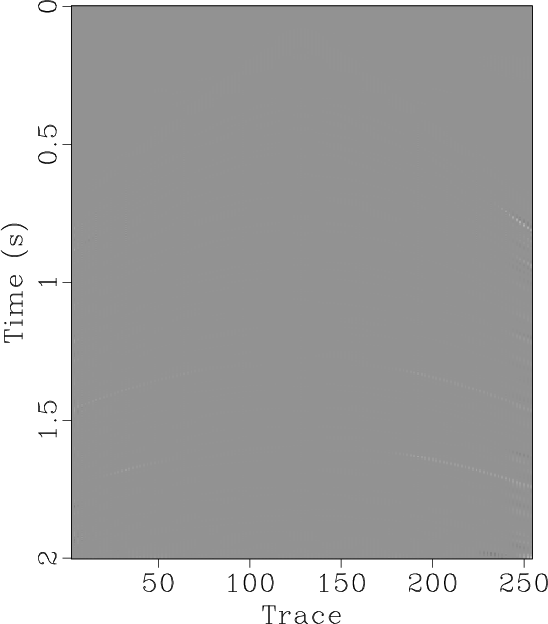
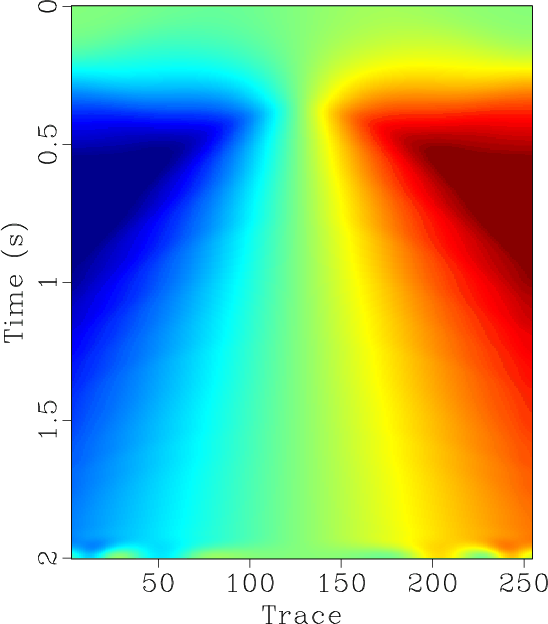
Figure 3. (a) Original synthetic data. (b) Decimated data (50% traces regularly removed). (c) |
|
|

|
|---|
|
hyper-seis,hyper-fx,fk-hyper-seis,fk-hyper-fx
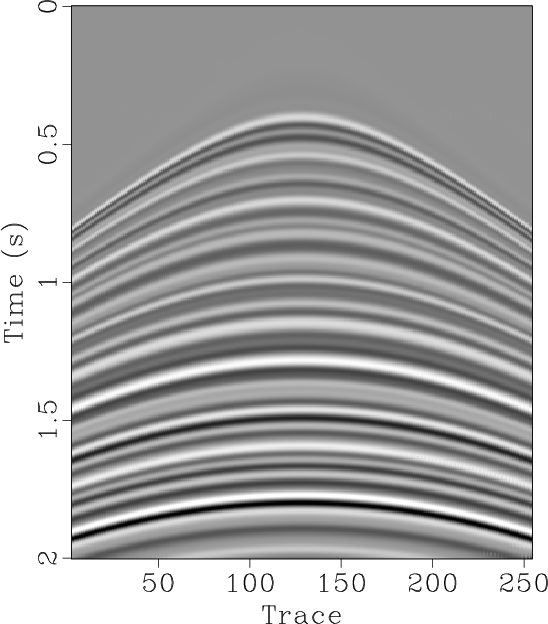
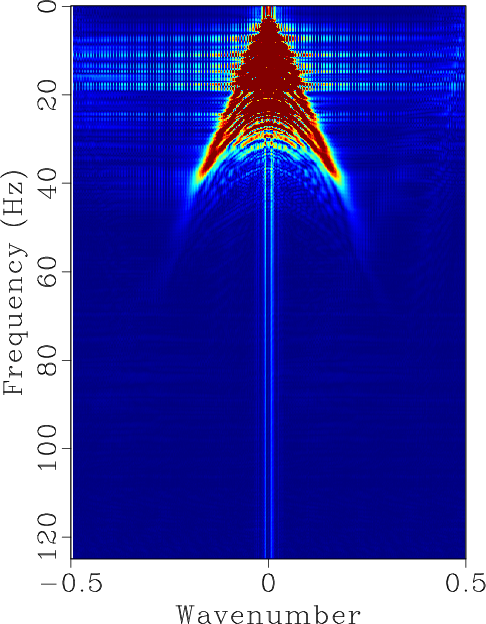
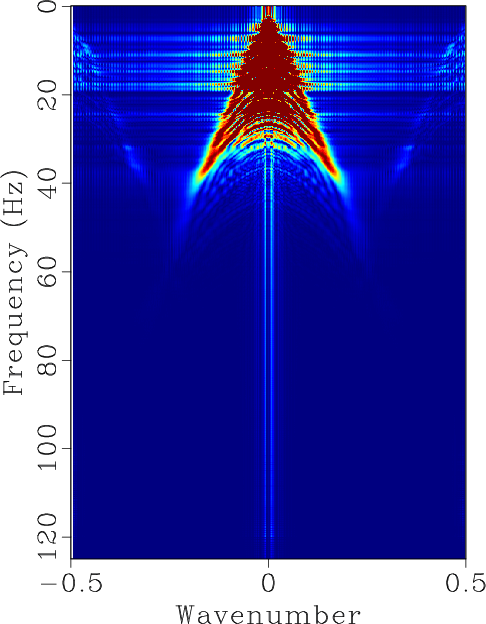
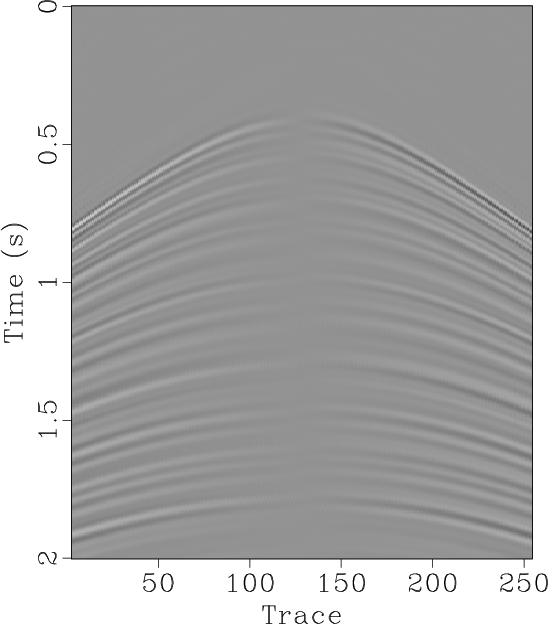
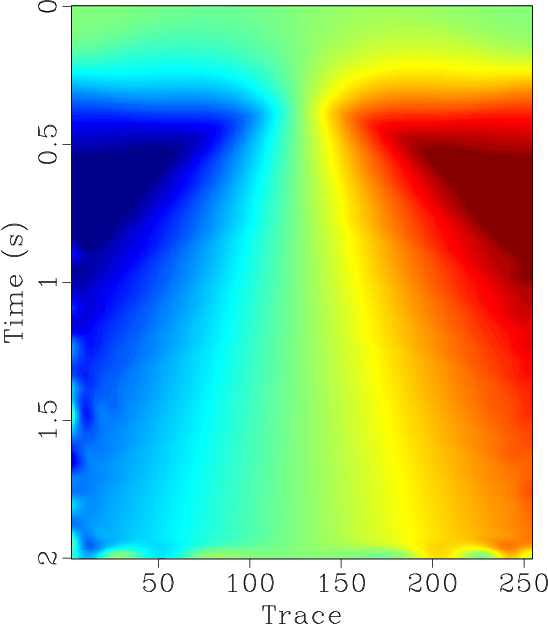
Figure 4. (a) Reconstructed data using the proposed approach. (b) Reconstructed data using Spitz's approach. (c) |
|
|
|
|---|
|
hyper-seis-dif,hyper-fx-dif
Figure 5. (a) Reconstruction error using the proposed approach. (b) Reconstruction error using the Spitz's approach. |
|
|
|
|---|
|
dip,dip1,dip2
Figure 6. (a) Accurate dip estimation. (b) Final dip estimation using 15 Hz low-pass filtering. (c) Final dip estimation using 30 Hz low-pass filtering. Note the aliased dip in (c). |
|
|
|
|---|
|
snrs-pocs
Figure 7. Convergence diagram of the first example using the proposed approach. |
|
|


|
|---|
|
linear,linear-zero,linear-seis,linear-fft
Figure 8. Second synthetic example test. (a) Original synthetic data. (b) Decimated data (50% traces regularly removed). (c) Reconstructed data using the proposed approach. (d) Reconstructed data using |
|
|
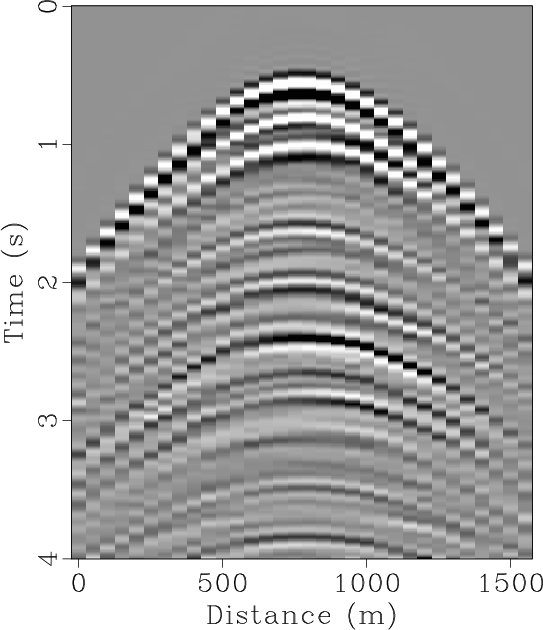
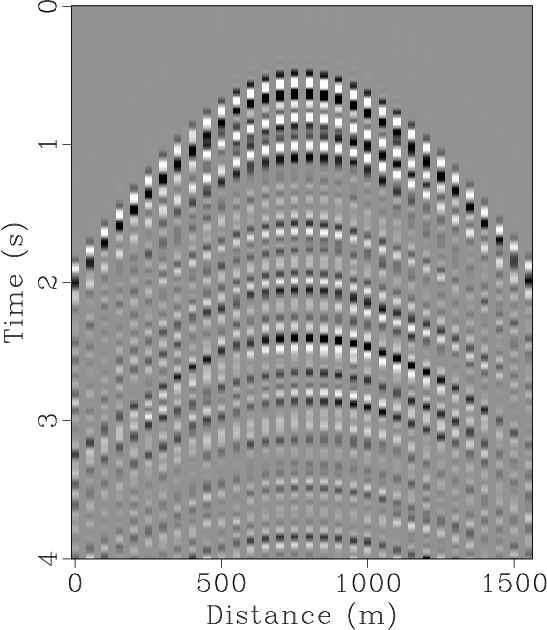
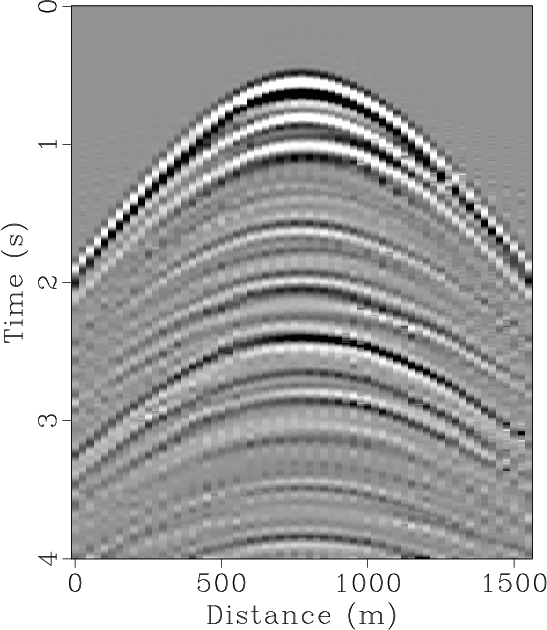
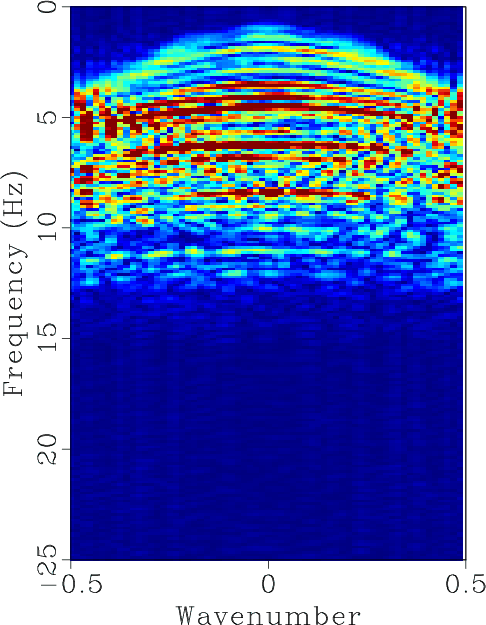
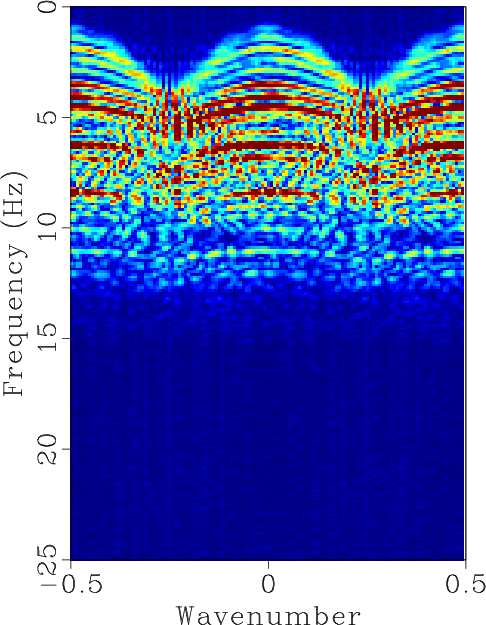
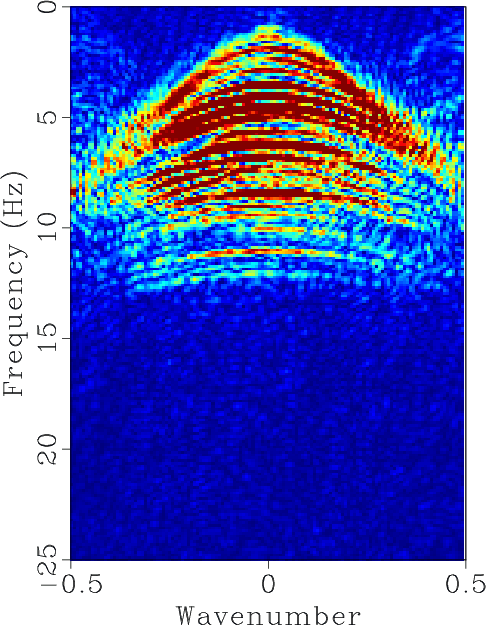
The field data example is a highly under-sampled common shot gather, as shown in Figure 9a. By manually adding zero traces between two neighbor traces, we obtain the zero-padded data, as shown in Figure 9b. After interpolation, a much better sampled data can be obtained, as shown in Figure 9c. In this example, we estimate the local slope using 5 Hz low-pass filtering. The corresponding ![]() spectrum are shown in Figures 9d, 9e and 9f, respectively. For many real seismic data, we might have difficulties to get the low-frequency information because of the low SNR at low frequencies. Thus, the proposed approach set a relatively high demand for data quality. Fortunately, we only require the low-frequency data for slope estimation and the appropriate frequency range varies from 5 Hz to 20 Hz for different datasets, which is not a problem for most field dataset.
spectrum are shown in Figures 9d, 9e and 9f, respectively. For many real seismic data, we might have difficulties to get the low-frequency information because of the low SNR at low frequencies. Thus, the proposed approach set a relatively high demand for data quality. Fortunately, we only require the low-frequency data for slope estimation and the appropriate frequency range varies from 5 Hz to 20 Hz for different datasets, which is not a problem for most field dataset.
|
|---|
|
field,field-zero,field-seis,fk-field,fk-field-zero,fk-field-seis
Figure 9. (a) Original field data. (b) Zero-padded field data. (c) Interpolated field data. (d) |
|
|