 |
 |
 |
 | A variational approach for picking optimal surfaces from semblance-like panels |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Decker & Fomel: Variational
Previous: Appendix A: Pseudocode for
Suppose we have a trace representative of a seismic horizon, apply cosine tapering to its edges, and pad it with zeros. This ideal horizon reference trace is called 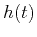 . To create a measure of how well this ideal waveform matches with other traces throughout a seismic volume, the crosscorrelation is calculated throughout the volume over shift
. To create a measure of how well this ideal waveform matches with other traces throughout a seismic volume, the crosscorrelation is calculated throughout the volume over shift 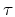 ,
,
 |
(9) |
where
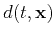 is the seismic image. In order to ensure that the volume we generate is non-negative, let
is the seismic image. In order to ensure that the volume we generate is non-negative, let
![$\displaystyle \alpha(\tau,\mathbf{x}) = \gamma(\tau,\mathbf{x}) - \min_{\left(\tau,\mathbf{x}\right)} \left[ \gamma(\tau,\mathbf{x})\right] .$](img135.png) |
(10) |
Automatic picking may be performed on the semblance-like volume
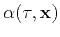 to determine the shifts defining the horizon corresponding to reference trace
to determine the shifts defining the horizon corresponding to reference trace 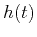 . Those shifts may be converted back to time in the image domain by adding a reference time for the ideal horizon trace, taken here to be that trace's midpoint.
. Those shifts may be converted back to time in the image domain by adding a reference time for the ideal horizon trace, taken here to be that trace's midpoint.
This is a basic method for creating a horizon probability volume, which is intended for use in this paper as part of a proof of concept for automatic horizon interpretation using the variational picking algorithm. It could encounter difficulties in areas where significant lateral wavelet variation or faulting occurs.
 |
 |
 |
 | A variational approach for picking optimal surfaces from semblance-like panels |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Decker & Fomel: Variational
Previous: Appendix A: Pseudocode for
2022-05-24