Semiautomatic Seismic Well-Ties

While the log data provides one source of information to understand the subsurface, an additional source of information is the 3D seismic dataset. Seismic-well ties can be used to calibrate seismic data, which has vertically lower resolution but higher spatial coverage, whereas the well logs can provide vertically higher resolution but are measured only at limited locations.

Synthetic seismograms are modeled independently for each well. White and Simm (2003) argue that modeling synthetic seismograms benefits from blocking or upscaling of the logs. Following their suggestion, we upscale the sonic and density logs to seismic frequencies (Backus, 1962; Marion et al., 1994) and estimate an initial reflectivity series, $r_0(z)$, in depth assuming no multiples, attenuation or dispersion.

$$r_0(z) = \frac{v_0(z + \Delta z)\rho(z + \Delta z) - v_0(z)\rho(z)}{v_0(z + \Delta z)\rho(z + \Delta z) + v_0(z)\rho(z)},$$ (9)

where $v_0$ is the initial, upscaled, P-wave velocity from sonic in $\frac{m}{s}$, $\rho$ is density in $\frac{gm}{cm^3}$, and $\Delta z$ is the sampling interval of the log in depth. To relate reflectivity in depth to seismic data in time, we must compute a time to depth relationship (TDR). There are several ways to compute a TDR. Using available checkshot surveys or vertical seismic profiles (VSP) can provide accurate measurements of seismic travel times to known depths; however, these surveys are not available to us, so we must estimate a TDR from well sonic logs. We define the initial TDR as a function of depth at each well,

$$T_0(z) = 2 \int_{z_{min}}^{z} \frac{d\xi}{v_0(\xi)},$$ (10)

where $T_0$ is the initial TDR, $z_{min}$ is the minimum depth at which sonic information is available, $v_0(z)$ is the initial, upscaled, P-wave velocity from sonic and $d\xi$ is the depth increment.

The initial TDR relates the initial reflectivity series, $r_0(z)$, to time. We interpolate the resulting reflectivity series in time to a regularly sampled grid of 0.002s, which corresponds to the vertical sampling of the seismic data.

$$r_0(t) = r_0(T_0(z))$$ (11)

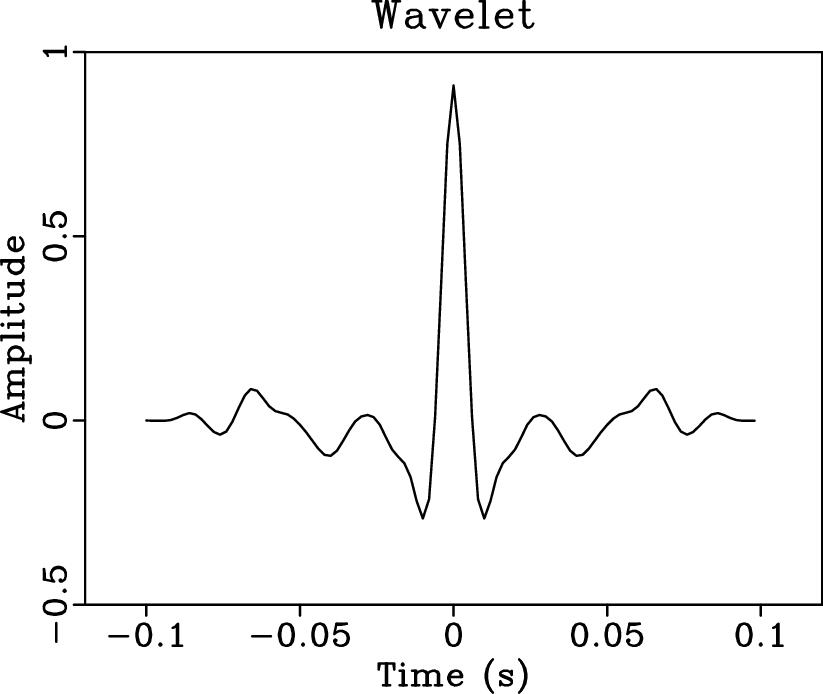
We model synthetic seismograms by convolving $r_0(t)$ with a single, zero-phase, wavelet that is representative of the seismic data's frequency content. The zero-phase wavelet extracted using Hampson Russell software is shown in Figure 13.

wavelet200
Figure 13. Statistical wavelet extracted from the Teapot Dome seismic dataset.

Using the statistical wavelet in Figure 13 and the initial TDR, we compute a synthetic seismogram shown in Figure 14 (green). We then iteratively estimate the alignment shifts, $g_{k}$, by using the LSIM method to match the synthetic seismogram (red) to the corresponding real seismic trace in Figure 14 (black).

In the time domain, the shifts, $g_{k,i}(t)$ at well $k$, are estimated using several iterations, $i$, of LSIM data matching. Each iteration estimates a smooth sequence of shifts to align the synthetic seismogram with the seismic trace. Muñoz and Hale (2015) and Herrera et al. (2014) observe a relationship between the shifts used to align a synthetic with seismic trace and an updated velocity function:

From Equation 2, assuming an initial TDR, $T_0$, we arrive at updated estimate

$$S_{k,1} (T_0) = T_0 + g_{k,1}(T_0)$$ (12)

after one iteration of LSIM. We estimate an updated TDR by interpolating our shifts from time to depth

$$T_1(z) = T_0(z) + g_{k,1}(T_0(z))$$ (13)

Using Equation 10, we relate the initial and updated velocity log to the initial and updated TDR,

$$\frac{dT_1(z)}{dz}\left(\frac{dT_0(z)}{dz}\right)^{-1} = \frac{v_0(z)}{v_1(z)}$$ (14)

to solve for the updated velocity log,

$$v_1(z) = v_0(z)\frac{dT_0(z)}{dz}\left(\frac{dT_1(z)}{dz}\right)^{-1}$$ (15)

In our implementation, we use Equation 15 to update the velocity function after each iteration. Alternatively, we can directly relate the updated velocity log to the initial velocity log and the estimated shifts. Starting with the derivative of Equation 13,

$$\frac{dT_1(z)}{dz} = \left(1 + \frac{g_{k,1}(T_0(z))}{dT_0}\right)\frac{dT_0(z)}{dz},$$ (16)

we substitute Equation 15 and solve for the update velocity log as follows,

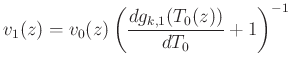$$v_1(z) = v_0(z)\left(\frac{dg_{k,1}(T_0(z))}{dT_0} + 1\right)^{-1}$$ (17)

We update the velocity function and recompute Equations 9, 10, and 11 after each iteration of estimating shifts using LSIM. We slowly reduce the smoothness enforced by regularization in LSIM with each iteration to ensure that stretching and squeezing are not excessive thus resulting in an improbable velocity update (White and Simm, 2003).

Prior to performing the seismic-well tie, we need to understand phase variations and distortions introduced during the processing and imaging of the seismic data. There are several seismic processing and imaging techniques that adjust or correct the seismic data to zero phase. Information on phase adjustments applied to the data are not available; however, Harbert (2012) interprets the deepest continuous reflection to be Precambrian basement resulting in a positive amplitude. As provided by the U.S. Department of Energy and RMOTC, the basement reflection is a negative amplitude. To account for the observed lateral and vertical phase variations, we apply local skewness correction (Fomel and van der Baan, 2014) resulting in a zero-phased seismic volume consistent with observations from Harbert (2012).