|
|
|
|
Forward interpolation |
It is interesting to note that many integral operators routinely used
in seismic data processing have the form of operator (25)
with the Green's function
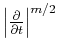 is defined
as the operator with the frequency response
is defined
as the operator with the frequency response
The impulse response (30) is typical for different forms
of Kirchhoff migration and datuming as well as for velocity transform,
integral offset continuation, DMO, and AMO. Integral operators of that
class rarely satisfy the unitarity condition, with the Radon transform
(slant stack) being a notable exception. In an earlier paper
(Fomel, 1996), I have shown that it is possible to define
the amplitude function ![]() for each kinematic path
for each kinematic path ![]() so that
the operator becomes asymptotically pseudo-unitary. This means
that the adjoint operator coincides with the inverse in the
high-frequency (stationary-phase) approximation. Consequently,
equation (28) is satisfied to the same asymptotic order.
so that
the operator becomes asymptotically pseudo-unitary. This means
that the adjoint operator coincides with the inverse in the
high-frequency (stationary-phase) approximation. Consequently,
equation (28) is satisfied to the same asymptotic order.
Using asymptotically pseudo-unitary operators, we can apply formula
(29) to find an explicit analytic form of the interpolation
function ![]() , as follows:
, as follows:
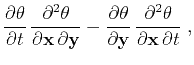 |
(33) | ||
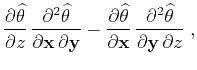 |
(34) |
For a simple example, let us consider the case of zero-offset time
migration with a constant velocity ![]() . The summation path
. The summation path ![]() in this case is an ellipse
in this case is an ellipse
While opening a curious theoretical possibility, seismic imaging
interpolants have an undesirable computational complexity. Following
the general regularization framework of Chapter ![]() , I
shift the computational emphasis towards appropriately chosen
regularization operators discussed in Chapter
, I
shift the computational emphasis towards appropriately chosen
regularization operators discussed in Chapter ![]() .
For the forward interpolation method, all data examples in this
dissertation use either the simplest nearest neighbor and linear
interpolation or a more accurate B-spline method, described in the
next section.
.
For the forward interpolation method, all data examples in this
dissertation use either the simplest nearest neighbor and linear
interpolation or a more accurate B-spline method, described in the
next section.
|
|
|
|
Forward interpolation |