|
|
|
|
Forward interpolation |
Unser et al. (1993) noticed that the basis function idea has an
especially simple implementation if the basis is convolutional and
satisfies the equation
According to the convolutional basis idea, forward interpolation
becomes a two-step procedure. The first step is the direct inversion
of equation (42): the basis coefficients ![]() are found by
deconvolving the sampled function
are found by
deconvolving the sampled function ![]() with the factorized filter
with the factorized filter
![]() . The second step reconstructs the continuous (or arbitrarily
sampled) function
. The second step reconstructs the continuous (or arbitrarily
sampled) function ![]() according to formula (41). The
two steps could be combined into one, but usually it is more
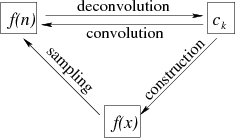
convenient to apply them separately. I show a schematic relationship
among different variables in Figure 12.
according to formula (41). The
two steps could be combined into one, but usually it is more
convenient to apply them separately. I show a schematic relationship
among different variables in Figure 12.
|
scheme
Figure 12. Schematic relationship among different variables for interpolation with a convolutional basis. |
|
|---|---|
|
|
|
|
|
|
Forward interpolation |