Waves in strata

Velocity increasing linearly with depth

Theoreticians are delighted by velocity increasing linearly with depth because it happens that many equations work out in closed form. For example, rays travel in circles. We will need convenient expressions for velocity as a function of traveltime depth and RMS velocity as a function of traveltime depth. Let us get them. We take the interval velocity 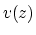$v(z)$ increasing linearly with depth:

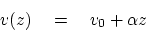$$v(z) \eq v_0 + \alpha z$$ (42)

This presumption can also be written as a differential equation:

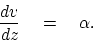$$\frac{dv}{dz} \eq \alpha .$$ (43)

The relationship between $z$ and vertical two-way traveltime $\tau(z)$ (see equation (3.27)) is also given by a differential equation:

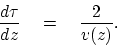$$\frac{d \tau}{dz} \eq \frac{2}{v(z)}.$$ (44)

Letting $v(\tau)=v(z(\tau))$ and applying the chain rule gives the differential equation for $v(\tau)$:

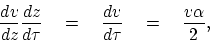$$\frac{dv}{dz} \frac{dz}{d \tau} \eq \frac{dv}{d \tau} \eq \frac{v \alpha}{2},$$ (45)

whose solution gives us the desired expression for interval velocity as a function of traveltime depth.

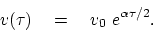$$v(\tau) \eq v_0 e^{\alpha \tau / 2 } .$$ (46)

Waves in strata