 |
 |
 |
 | Elastic wave-mode separation for VTI media |  |
![[pdf]](icons/pdf.png) |
Next: Operator size and compactness
Up: Operator properties
Previous: Operator properties
As I have showed in the previous section, the isotropic separation
operators (divergence and curl) in equations 4 and 5 are
exact in the  and
and 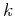 domains.
The exact derivative operators are infinitely long
series in the discretized space domain. In practice, when
evaluating the derivatives numerically, one needs to take some
approximations to make the operators short and computationally
efficient. Usually, difference operators are evaluated at different
orders of accuracy. The higher order the approximation is, the more
accurate and longer the operator becomes. For example, the
domains.
The exact derivative operators are infinitely long
series in the discretized space domain. In practice, when
evaluating the derivatives numerically, one needs to take some
approximations to make the operators short and computationally
efficient. Usually, difference operators are evaluated at different
orders of accuracy. The higher order the approximation is, the more
accurate and longer the operator becomes. For example, the 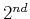 order operator has coefficients
order operator has coefficients
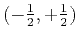 , and the
more accurate
, and the
more accurate 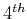 order operator has coefficients
order operator has coefficients
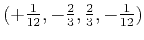 (Fornberg and Ghrist, 1999).
(Fornberg and Ghrist, 1999).
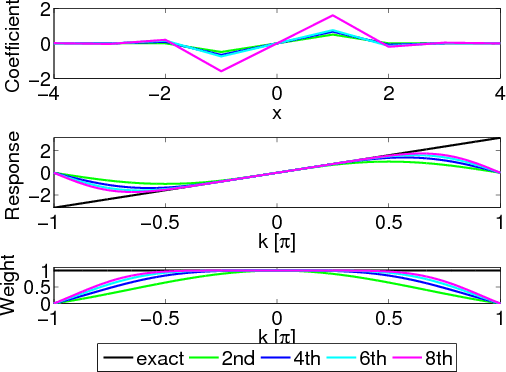
In the wavenumber domain, for isotropic media, as shown by the black
line in Figure 2(b), the exact difference operator is 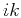 .
Appendix A shows the
.
Appendix A shows the 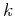 domain equivalents of the
domain equivalents of the 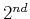 ,
, 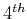 ,
,
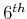 , and
, and 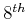 order finite difference operators, and they are
plotted in Figure 2(b). The higher order operators have
responses closer to the exact operator
order finite difference operators, and they are
plotted in Figure 2(b). The higher order operators have
responses closer to the exact operator 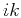 (black line). To obtain
vertical and horizontal derivatives of different orders of accuracy,
I weight the polarization vector
(black line). To obtain
vertical and horizontal derivatives of different orders of accuracy,
I weight the polarization vector
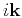 components
components 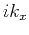 and
and  by the weights shown in Figure 2(c). For VTI media, similarly,
I weight the anisotropic polarization vector
by the weights shown in Figure 2(c). For VTI media, similarly,
I weight the anisotropic polarization vector
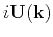 components
components
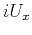 and
and  by these same weights. The weighted vectors are then
transformed back to space domain to obtain the anisotropic stencils.
by these same weights. The weighted vectors are then
transformed back to space domain to obtain the anisotropic stencils.
|
|---|
operator
Figure 2. Comparison of
derivative operators of different orders of accuracy (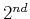 ,
,
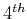 ,
, 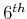 , and
, and 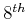 orders in space, as well as the
approximation applied in Dellinger and Etgen (1990)-cosine taper)
in both (a) the
orders in space, as well as the
approximation applied in Dellinger and Etgen (1990)-cosine taper)
in both (a) the  domain and (b) the
domain and (b) the 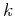 domain. (c) Weights to
apply to the components of the polarization vectors.
domain. (c) Weights to
apply to the components of the polarization vectors.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[matlab]](icons/matlab.png)
|
|---|








|
|---|
iop2,mop2,iop4,mop4,iop6,mop6,iop8,mop8
Figure 3. 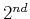 ,
, 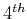 ,
, 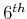 , and
, and 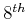 order derivative operators for an isotropic medium (
order derivative operators for an isotropic medium (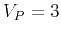 km/s and
km/s and
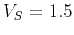 km/s) and a VTI medium (
km/s) and a VTI medium (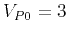 km/s,
km/s,
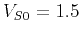 km/s,
km/s,
 and
and
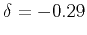 ). The left column includes
isotropic operators, and the right column includes anisotropic
operators. From top to bottom are operators with increasing orders of
accuracy.
). The left column includes
isotropic operators, and the right column includes anisotropic
operators. From top to bottom are operators with increasing orders of
accuracy.
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
 |
 |
 |
 | Elastic wave-mode separation for VTI media |  |
![[pdf]](icons/pdf.png) |
Next: Operator size and compactness
Up: Operator properties
Previous: Operator properties
2013-08-29
![]() .
Appendix A shows the
.
Appendix A shows the ![]() domain equivalents of the
domain equivalents of the ![]() ,
, ![]() ,
,
![]() , and
, and ![]() order finite difference operators, and they are
plotted in Figure 2(b). The higher order operators have
responses closer to the exact operator
order finite difference operators, and they are
plotted in Figure 2(b). The higher order operators have
responses closer to the exact operator ![]() (black line). To obtain
vertical and horizontal derivatives of different orders of accuracy,
I weight the polarization vector
(black line). To obtain
vertical and horizontal derivatives of different orders of accuracy,
I weight the polarization vector
![]() components
components ![]() and
and ![]() by the weights shown in Figure 2(c). For VTI media, similarly,
I weight the anisotropic polarization vector
by the weights shown in Figure 2(c). For VTI media, similarly,
I weight the anisotropic polarization vector
![]() components
components
![]() and
and ![]() by these same weights. The weighted vectors are then
transformed back to space domain to obtain the anisotropic stencils.
by these same weights. The weighted vectors are then
transformed back to space domain to obtain the anisotropic stencils.








