|
|
|
|
Elastic wave-mode separation for VTI media |
Figure 4
shows anisotropic derivative operators with
same order of accuracy (![]() order in space) for three VTI media
with different combinations of
order in space) for three VTI media
with different combinations of ![]() and
and ![]() . These
operators have similar central parts, but different outer parts. This
result is consistent with the previous observation that the central
part of an operator is determined by the order of accuracy, and the
outer part is controlled by anisotropy parameters.
. These
operators have similar central parts, but different outer parts. This
result is consistent with the previous observation that the central
part of an operator is determined by the order of accuracy, and the
outer part is controlled by anisotropy parameters.
Figure 5(a) shows the influence of
approximation to finite difference (![]() and
and ![]() order, Figures 3(h) and fig:oporder-mop2). The ``anisotropic''
part (``diagonal tails'') are almost the same, and the difference comes from
the central part. Figure 5(b) shows the difference
between operators with different anisotropy (Figures 4(a)
and fig:aniopsize-mop1-order8). The difference mainly lies in the ``tails''
of the operators.
order, Figures 3(h) and fig:oporder-mop2). The ``anisotropic''
part (``diagonal tails'') are almost the same, and the difference comes from
the central part. Figure 5(b) shows the difference
between operators with different anisotropy (Figures 4(a)
and fig:aniopsize-mop1-order8). The difference mainly lies in the ``tails''
of the operators.
A comparison between Figures 4(a)
and fig:aniopsize-mop1-order8 shows that when one has large
difference between ![]() and
and ![]() , the operator is big in
size and when the difference of
, the operator is big in
size and when the difference of ![]() and
and ![]() stays the
same, the parameter
stays the
same, the parameter ![]() affects the operator size. A comparison
between Figures 4(b) and fig:aniopsize-mop2-order8
shows that when the difference between
affects the operator size. A comparison
between Figures 4(b) and fig:aniopsize-mop2-order8
shows that when the difference between ![]() and
and ![]() becomes
smaller and
becomes
smaller and ![]() does not change, the operator get smaller in
size. This result is consistent with the polarization equation for VTI
media with weak anisotropy (Tsvankin, 2005):
does not change, the operator get smaller in
size. This result is consistent with the polarization equation for VTI
media with weak anisotropy (Tsvankin, 2005):
| (10) |
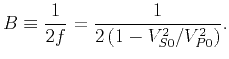



|
|---|
|
mop0-order8,mop1-order8,mop2-order8
Figure 4. |
|
|


|
|---|
|
diff0,diff1
Figure 5. (a) The difference between the |
|
|
|
|
|
|
Elastic wave-mode separation for VTI media |