|
|
|
|
Elastic wave-mode separation for VTI media |
The derivative operators for isotropic and anisotropic media are very
different in both shape and size , and the operators vary with
the strength of anisotropy. In theory, analytic isotropic derivatives
are point operators in the continuous limit. If one can do
perfect Fourier transform to ![]() and
and ![]() (without doing the
approximations to different orders of accuracy as one does
in Figure 2), one gets point derivative operators. This is because
(without doing the
approximations to different orders of accuracy as one does
in Figure 2), one gets point derivative operators. This is because
![]() is constant in the
is constant in the ![]() direction (see Figure 6(a)), whose
Fourier transform is delta function; the exact expression of
direction (see Figure 6(a)), whose
Fourier transform is delta function; the exact expression of ![]() in the
in the ![]() domain also makes the operator point in the
domain also makes the operator point in the ![]() direction. This makes the isotropic derivative operators point
operators in the
direction. This makes the isotropic derivative operators point
operators in the ![]() and
and ![]() direction. And when one applies
approximations to the operators, they are compact in the space domain.
direction. And when one applies
approximations to the operators, they are compact in the space domain.
However, even if one does perfect Fourier transformation to ![]() and
and
![]() (without doing the approximations for different orders of
accuracy) for VTI media, the operators will not be point operators
because
(without doing the approximations for different orders of
accuracy) for VTI media, the operators will not be point operators
because ![]() and
and ![]() are not constants in
are not constants in ![]() and
and ![]() directions,
respectively (see Figure 6(b)). The
directions,
respectively (see Figure 6(b)). The ![]() domain operators spread out in
all directions (Figures 3(b), fig:mop4, fig:mop6,
and fig:mop8).
domain operators spread out in
all directions (Figures 3(b), fig:mop4, fig:mop6,
and fig:mop8).
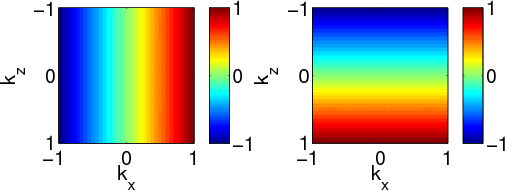
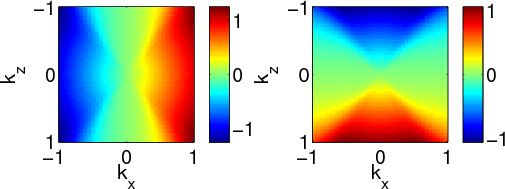
|
|---|
|
IsoU,AniU
Figure 6. (a) Isotropic and (b) VTI ( |
|
|
This effect is illustrated by Figure 3. When the order of accuracy decreases, the isotropic operators become more compact (shorter in space), while the anisotropic operators do not get more compact. No matter how one improves the compactness of isotropic operators, one does not get compact anisotropic operators in the space domain by the same means.
Because the size of the anisotropic derivative operators is usually
large, it is natural that one would truncate the operators to save
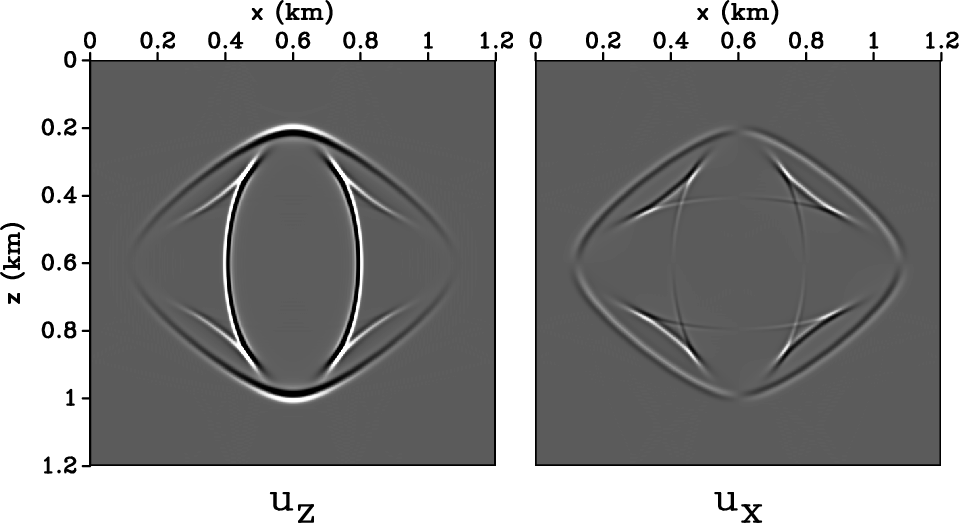
computation. Figure 7 shows a snapshot of an elastic wavefield
and corresponding derivative operators for a VTI medium with
![]() and
and
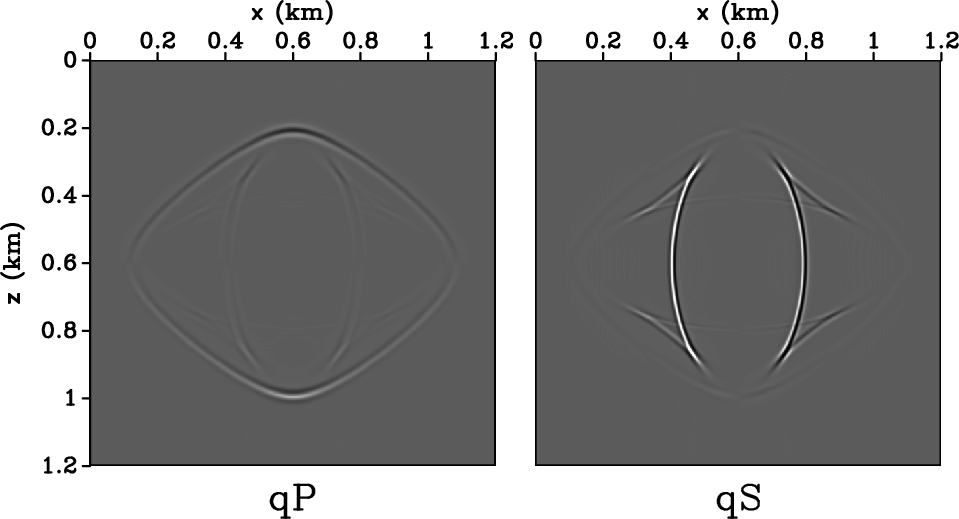
![]() . Figure 8 shows the
attempt of separation using truncated operator size of (a)
. Figure 8 shows the
attempt of separation using truncated operator size of (a)
![]() , (b)
, (b)
![]() and (c)
and (c)
![]() out of the full
operator size
out of the full
operator size
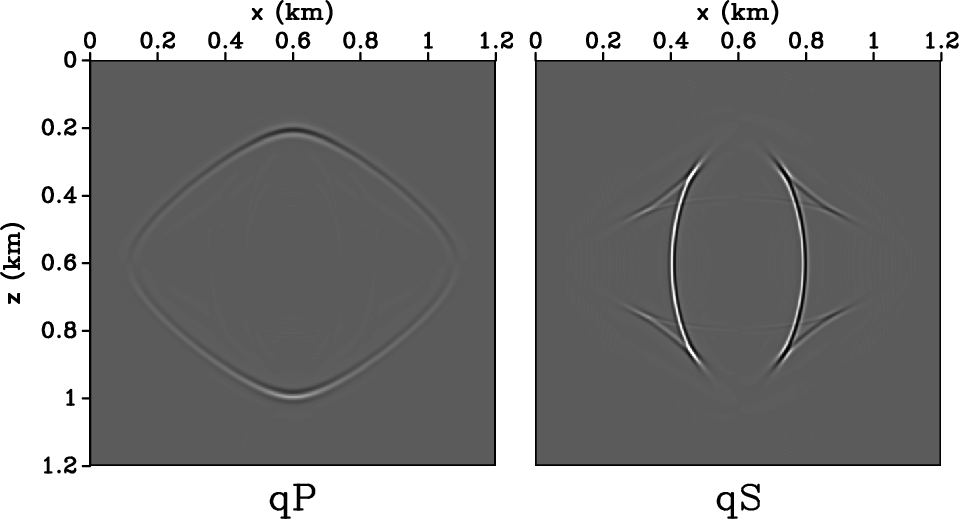
![]() . Figure 8 shows that the truncation
causes the wave-modes incompletely separated. This is because the
truncation changes the directions of the polarization vectors, thus
projecting the wavefield displacements onto wrong directions.
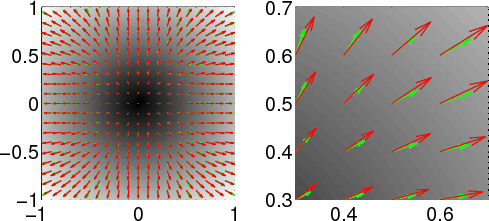
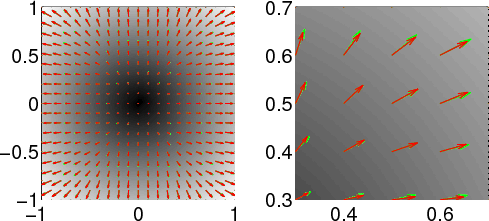
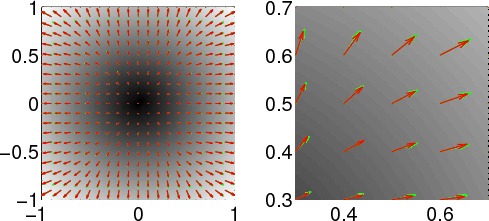
Figure 9 presents
the P-wave polarization vectors before and after the truncation. For
a truncated operator size of
. Figure 8 shows that the truncation
causes the wave-modes incompletely separated. This is because the
truncation changes the directions of the polarization vectors, thus
projecting the wavefield displacements onto wrong directions.
Figure 9 presents
the P-wave polarization vectors before and after the truncation. For
a truncated operator size of
![]() , the polarization vectors
deviate from the correct ones to a maximum of 10
, the polarization vectors
deviate from the correct ones to a maximum of 10![]() , but
even this difference makes the separation incomplete.
, but
even this difference makes the separation incomplete.

|
|---|
|
uA,mop5
Figure 7. (a) A snapshot of an elastic wavefield showing the vertical (left) and horizontal (right) components for a VTI medium ( |
|
|

|
|---|
|
pA1,pA3,pA5
Figure 8. separation by |
|
|
|
|---|
|
truncate1,truncate2,truncate3
Figure 9. The deviation of polarization vectors by truncating the size of the space-domain operator to (a) |
|
|
|
|
|
|
Elastic wave-mode separation for VTI media |