VD-slope pattern for pegleg multiples

Next: Separation of primaries and Up: Theory Previous: VD-slope pattern for primary

VD-slope pattern for pegleg multiples

In a laterally homogeneous model, the NMO equation 6 flattens primary events on a CMP gather with offset 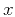and time to its zero-offset traveltime . Brown and Guitton (2005) use an analogous NMO equation for pegleg multiples under locally 1D earth assumption. For example, first-order pegleg can be kinematically approximated by pseudo-primary with the same offset but with an additional zero-offset traveltime $\tau$ . The NMO equation for an th-order pegleg multiple is generalized to

$\begin{displaymath} t_m(x) = \sqrt{(t_0+m\tau)^2 + \frac{x^2}{v_m^2(t_0)}}\;, \end{displaymath}$

(8)

where

is the corresponding multiple traveltime recorded at offset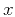

and the effective RMS velocity

is defined according to Dix's equation as:

$\begin{displaymath} v_m(t_0) = \sqrt{\frac{t_0v^2(t_0)+m\tau\,v^2(\tau)}{t_0+m\tau}}\;. \end{displaymath}$

(9)

In marine seismic data, $v(\tau)$ is constant water velocity, and it assumes that we are able to pick zero-offset traveltime $\tau$ of the water bottom. According to the definition of slopes for primaries (equation 7), slopes for pegleg multiples can be calculated analogously by:

$\begin{displaymath} \sigma_m(t,x) = {\frac{x}{t_m(x)\,v_m^2(t_0,x)}}\;. \end{displaymath}$

(10)

Equation 10 provides the estimation of multiple slopes, which we use to define VD-seislet frame for representing pegleg multiples of different orders.

Next: Separation of primaries and Up: Theory Previous: VD-slope pattern for primary

2015-10-24