Signal and noise separation in prestack seismic data using velocity-dependent seislet transform

Separation of primaries and pegleg multiples using VD-seislet frame

Once the VD-seislet transform is defined, it can be applied to analyze signals composed of multiple wavefields, e.g., primaries and multiples of different orders. If a range of slopes are chosen and a VD-seislet transform is constructed for each of them, then all the transforms together will constitute an overcomplete representation. Mathematically, if $\mathbf{F}_i$ is the VD-seislet transform for the $i$th slope pattern (corresponding to primaries or pegleg multiples of different orders), then, for any data vector $\mathbf{d}$,

$$\sum\limits_{i=1}^N \Vert\mathbf{F}_i\,\mathbf{d}\Vert^2 = ... ..._{i=1}^N \Vert\mathbf{d}\Vert^2 = N\,\Vert\mathbf{d}\Vert^2\;,$$ (11)

which means that all transforms taken together constitute a tight frame with constant $N$ (Mallat, 2009).

Because of its overcompleteness, a frame representation for a given signal is not unique. In order to assure that different wavefield components do not leak into other parts of the frame, it is advantageous to employ sparsity-promoting inversion (Fomel and Liu, 2010). We use a nonlinear shaping-regularization scheme (Fomel, 2008) and define sparse decomposition as an iterative thresholding process (Daubechies et al., 2004)

$$\hat{\mathbf{f}}_{k+1} = \mathbf{S}[\mathbf{F}\, \mathbf{d}+(\mathbf{I}-\mathbf{F}\, \mathbf{B})\,\hat{\mathbf{f}}_{k}]\;,$$ (12)

$$\mathbf{f}_{k+1} = \mathbf{f}_k + \mathbf{F}\, \mathbf{d}- \mathbf{F}\,\mathbf{B} \hat{\mathbf{f}}_{k+1}\;,$$ (13)

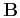where $\mathbf{f}_k$ are coefficients of the seislet frame at $k$th iteration, $\hat{\mathbf{f}}_k$ is an auxiliary quantity, $\mathbf{S}$ is a soft thresholding operator, $\mathbf{F}$ and $\mathbf{B}$ are frame construction and deconstruction operators

$$\mathbf{F} \equiv \left[\begin{array}{cccc}\mathbf{F}_1 &\mathbf{F}_2 & \cdots &\mathbf{F}_N\end{array}\right]^T\;,$$ (14)

$$\mathbf{B} \equiv \left[\begin{array}{cccc}\mathbf{F}_1^{-1} &\mathbf{F}_2^{-1} & \cdots &\mathbf{F}_N^{-1}\end{array}\right]\;.$$ (15)

The iteration in equations 12 and 13 starts with $\mathbf{f}_0=\mathbf{0}$ and $\hat{\mathbf{f}_0}=\mathbf{F}\mathbf{d}$ and is related to the linearized Bregman iteration (Cai et al., 2009), which converges to the solution of the constrained minimization problem:

$$\min_{\mathbf{f}}\Vert\mathbf{f}\Vert _1 \; s.t.\; \mathbf{Bf} = \mathbf{d}\;.$$ (18)

Separated wavefield can be calculated by $\mathbf{d}_i=\mathbf{B}\mathbf{M}_i\mathbf{f}_\eta$, where $\eta$ is iteration number, masking operator $\mathbf{M}_i$ is a diagonal matrix as

$$\mathbf{M}_i = \left[\begin{array}{ccccccc} \mathbf{0} ... ...ts & \cdots & \mathbf{0}\\ \end{array}\right]_{N\times N}\;,$$ (19)

and $\mathbf{d}_i$ corresponds to the signal of interest (e.g., primaries or multiples of selected order). We calculate all patterns for primaries and multiples, and then apply sparse decomposition (equations 12 and 13) to separate primaries from multiples. In practice, a small number of iterations is usually sufficient for convergence and for achieving both model sparseness and data recovery.

Signal and noise separation in prestack seismic data using velocity-dependent seislet transform