 |
 |
 |
 | Asymptotic pseudounitary stacking operators |  |
![[pdf]](icons/pdf.png) |
Next: Conclusions
Up: EXAMPLES
Previous: Velocity Transform
Offset continuation is the operator that transforms seismic reflection
data from one offset to another
(Bolondi et al., 1982; Salvador and Savelli, 1982). If the data are continued
from half-offset  to a larger offset
to a larger offset 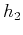 , the summation path of
the post-NMO integral offset continuation has the following form
(Stovas and Fomel, 1996; Fomel, 2001b; Biondi and Chemingui, 1994):
, the summation path of
the post-NMO integral offset continuation has the following form
(Stovas and Fomel, 1996; Fomel, 2001b; Biondi and Chemingui, 1994):
 |
(73) |
where
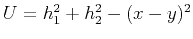 ,
,
 , and
, and 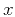 and
and 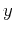 are the midpoint coordinates before and
after the continuation. The summation path of the reverse continuation
is found from inverting (73) to be
are the midpoint coordinates before and
after the continuation. The summation path of the reverse continuation
is found from inverting (73) to be
 |
(74) |
The Jacobian of the time coordinate transformation in this case is simply
 |
(75) |
Differentiating summation paths (73) and (74), we
can define the product of the weighting functions according to formula
(10), as follows:
 |
(76) |
The weighting functions of the amplitude-preserving offset
continuation have the form (Fomel, 2001b)
It easy to verify that they satisfy relationship (76);
therefore, they appear to be asymptotically inverse to each other.
The weighting functions of the asymptotic pseudo-unitary offset
continuation are defined from formulas (28) and (29), as follows:
The most important case of offset continuation is the continuation
to zero offset. This type of continuation is known as dip moveout
(DMO). Setting the initial offset  equal to zero in the general
offset continuation formulas, we deduce that the inverse and forward
DMO operators have the summation paths
equal to zero in the general
offset continuation formulas, we deduce that the inverse and forward
DMO operators have the summation paths
The weighting functions of the amplitude-preserving inverse and
forward DMO are
and the weighting functions of the asymptotic pseudo-unitary DMO are
Equations similar to (83) and (84) have
been published by Stovas and Fomel (1996). Equation (84) differs
from the similar result of Black et al. (1993) by a simple time
multiplication factor. This difference corresponds to the difference
in definition of the amplitude preservation criterion.
Equation (84) agrees asymptotically with the
frequency-domain Born DMO operators
(Bleistein and Cohen, 1995; Bleistein, 1990; Liner, 1991). Likewise, the stacking operator
with the weighting function (83) corresponds to Ronen's
inverse DMO (Ronen, 1987), as discussed by
Fomel (2001b). Its adjoint, which has the weighting
function
 |
(87) |
corresponds to Hale's DMO (Hale, 1984).
 |
 |
 |
 | Asymptotic pseudounitary stacking operators |  |
![[pdf]](icons/pdf.png) |
Next: Conclusions
Up: EXAMPLES
Previous: Velocity Transform
2013-03-03
![]() equal to zero in the general
offset continuation formulas, we deduce that the inverse and forward
DMO operators have the summation paths
equal to zero in the general
offset continuation formulas, we deduce that the inverse and forward
DMO operators have the summation paths