 |
 |
 |
 | Asymptotic pseudounitary stacking operators |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Asymptotic pseudounitary stacking operators
Previous: Conclusions
I owe my familiarity with the asymptotic inversion theory to Sergey
Goldin. A short discussion with Martin Tygel helped me better
understand the true-amplitude migration concept.
I thank Jon Claerbout for helpful discussions and the sponsors of the Stanford
Exploration Project for the financial support of this work. Comments
from three anonymous reviewers helped to improve the paper.
Appendix
A
Least-squares Radon transform inversion
This appendix exemplifies the application of adjoint operators by
reviewing the analytical least-squares inversion of the classic Radon
transform (slant stack operator).
Forming the product
 for this case leads
to the double integral
for this case leads
to the double integral
Applying Fourier transform with respect to  , we can rewrite
equation (A-1) in the frequency domain as
, we can rewrite
equation (A-1) in the frequency domain as
 |
(89) |
where
The inner integral in equation (A-2) reduces to the  -dimensional
delta function:
-dimensional
delta function:
 |
(92) |
As follows from the properties of delta function,
 |
(93) |
Inverting (A-6) for 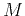 , we conclude that
, we conclude that
 |
(94) |
Substituting equation (A-7) into (13) produces
the result precisely equivalent to Radon's
inversion (4).
 |
 |
 |
 | Asymptotic pseudounitary stacking operators |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Asymptotic pseudounitary stacking operators
Previous: Conclusions
2013-03-03
![]() for this case leads
to the double integral
for this case leads
to the double integral


