 |
 |
 |
 | Asymptotic pseudounitary stacking operators |  |
![[pdf]](icons/pdf.png) |
Next: ASYMPTOTIC INVERSION: RECONSTRUCTING THE
Up: Asymptotic pseudounitary stacking operators
Previous: Introduction
In practice, integration of discrete data is performed by stacking.
In theory, it is convenient to
represent a stacking operator in the form of a continuous integral:
![$\displaystyle S(t,y)= {\bf A}\left[M(z,x)\right]= \int\limits_{\Omega} w(x;t,y) M(\theta(x;t,y),x) dx\;.$](img1.png) |
(1) |
Function 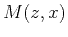 is the input of the operator,
is the input of the operator, 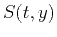 is the
output,
is the
output, 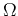 is the summation aperture,
is the summation aperture,
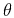 represents the summation path, and
represents the summation path, and 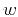 stands for the
weighting function. The range of integration (the
operator aperture) may also depend on
stands for the
weighting function. The range of integration (the
operator aperture) may also depend on  and
and 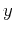 . Allowing
. Allowing 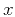 to be
a two-dimensional variable, we can use definition (1) to
represent an operator applied to three-dimensional data. Throughout
this paper, I assume that
to be
a two-dimensional variable, we can use definition (1) to
represent an operator applied to three-dimensional data. Throughout
this paper, I assume that  and
and  belong to a one-dimensional
space, and that
belong to a one-dimensional
space, and that 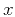 and
and 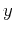 have the same number of dimensions.
have the same number of dimensions.
The goal of inversion is to reconstruct some function
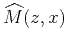 for a given
for a given 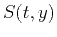 , so that
, so that
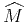 is in some
sense close to
is in some
sense close to 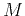 in equation (1).
in equation (1).
 |
 |
 |
 | Asymptotic pseudounitary stacking operators |  |
![[pdf]](icons/pdf.png) |
Next: ASYMPTOTIC INVERSION: RECONSTRUCTING THE
Up: Asymptotic pseudounitary stacking operators
Previous: Introduction
2013-03-03
![]() for a given
for a given ![]() , so that
, so that
![]() is in some
sense close to
is in some
sense close to ![]() in equation (1).
in equation (1).