First-break traveltime tomography with the double-square-root eikonal equation

DSR eikonal equation

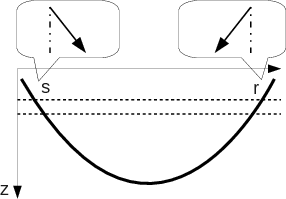
The DSR eikonal equation can be derived by considering a ray-path and its segments between two depth levels. Figure 1 illustrates a diving ray (Zhu et al., 1992) in 2-D with velocity $v = v (z,x)$. We denote $T (z,r,s)$ as the total traveltime of the ray-path beneath depth $z$, where $r$ and $s$ are sub-surface receiver and source lateral positions, respectively.

raypath
Figure 1. A diving ray and zoom-in of the ray segments between two depth levels.

At both source and receiver sides the traveltime satisfies the eikonal equation, therefore

$$\frac{\partial T}{\partial z} = - \sqrt{\frac{1}{v^2 (z,s)}... ...{v^2 (z,r)}-\left( \frac{\partial T}{\partial r} \right)^2}\;.$$ (1)

The negative signs before the two square-roots in equation 1 correspond to a decrease of traveltime with increasing depth, or geometrically a downward pointing of slowness vectors on both $s$ and $r$ sides. Since the slowness vectors could also be pointing upward and the directions may be different at $r$ and $s$, the DSR eikonal equation (Belonosova and Alekseev, 1974) should account for all the possibilities (Figure 2):

$$\frac{\partial T}{\partial z} = \pm \sqrt{\frac{1}{v^2 (z,s... ...{v^2 (z,r)}-\left( \frac{\partial T}{\partial r} \right)^2}\;.$$ (2)

The boundary condition for DSR eikonal equation is that traveltimes at the subsurface zero-offset plane, i.e. $r = s$, are zero: $T (z,r=s) = 0$.

Equation 2 has a singularity when $\partial T / \partial z = 0$, in which case the slowness vectors at $s$ and $r$ sides are both horizontal and equation 2 reduces to

$$\left( \frac{\partial T}{\partial s} \right)^2 = \frac{1}{v^... ...rac{\partial T}{\partial r} \right)^2 = \frac{1}{v^2 (z,r)}\;.$$ (3)

The two independent equations in 3 are not in conflict according to the source-receiver reciprocity, because they are the same with an exchange of $s$ and $r$.

Note that equations 2 and 3 describe $T$ in full prestack domain $(z,r,s)$ by allowing not only receivers but also sources to change positions. In contrast, the eikonal equation

$$\left( \frac{\partial T}{\partial z} \right)^2 + \left( \frac{\partial T}{\partial x} \right)^2 = \frac{1}{v^2 (z,x)}$$ (4)

with boundary condition $T (z=0,x=s) = 0$ can be used only for one fixed source position at a time and thus traveltimes of different shots are independent of each other. In equation 4 $s$ is surface source lateral position. In the 3-D case, the scalars $s$, $r$ and $x$ in equations 2, 3 and 4 become 2-D vectors $\mathbf{s}$, $\mathbf{r}$ and $\mathbf{x}$ that contain in-line and cross-line positions. The prestack traveltime is then in a 5-D space. Our current work is restricted to 2-D and we consider the 3-D extension in the Discussion section.

root
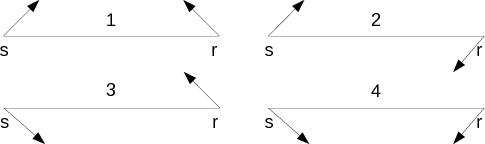
Figure 2. All four branches of DSR eikonal equation from different combination of upward or downward pointing of slowness vectors. Whether the slowness vector is pointing leftward or rightward does not matter because the partial derivatives with respect to $s$ and $r$ in equation 2 are squared. Figure 1 and equation 1 belong to the last situation.

Similarly to the eikonal equation, the DSR eikonal equation is a nonlinear first-order partial differential equation. Its solutions include in general not only first-breaks but all arrivals, and can be computed by solving separate eikonal equations for each sub-surface source-receiver pair followed by extracting the traveltime and putting the value into prestack volume. However, such an implementation is impractical due to the large amount of computations. Meanwhile, for first-break tomography purposes, we are only interested in the first-arrival solutions but require an efficient and accurate algorithm. In this regard, a finite-difference DSR eikonal solver analogous to the fast-marching (Sethian, 1999) or fast-sweeping (Zhao, 2005) eikonal solvers is preferable.

In upwind discretizations of the DSR eikonal equation on the grid in $(z,r,s)$ domain, one has to make a decision about the $z$-slice, in which the finite differences are taken to approximate $\partial T / \partial s$ and $\partial T / \partial r$. In Figure 1, it appears natural to approximate these partial derivatives in the $z$-slice below $T (z,r,s)$. We refer to the corresponding scheme as explicit, since it allows to directly compute the grid value $T (z,r,s)$ based on the already known $T$ values from the next-lower $z$. An alternative implicit scheme is obtained by approximating $\partial T / \partial s$ and $\partial T / \partial r$ in the same $z$-slice as $T (z,r,s)$, which results in a coupled system of nonlinear discretized equations. In Appendix A, we prove the following:

1. The explicit scheme is very efficient to use on a fixed grid, but only conditionally convergent. This property is also confirmed numerically in Synthetic Model Examples section.
2. The implicit scheme is monotone causal, meaning $T (z,r,s)$ depends on the smaller neighboring grid values only. This enables us to apply a Dijkstra-like method (Dijkstra, 1959) to solve the discretized system efficiently. Importantly, the DSR singularity requires a special ordering in the selection of upwind neighbors, which switches between equations 1 and 3 when necessary. We provide a modified fast-marching (Sethian, 1999) DSR eikonal solver along with such an ordering strategy in Numerical Implementation section.
3. The causality analysis in Appendix A applies only to the first and last causal branches out of all four shown in Figure 2. Additional post-processings, albeit expensive, can be used to recover the rest two non-causal branches as they may be decomposed into summations of the causal ones.

In practice, we find that, for moderate velocity variations, the first-breaks correspond only to causal branches. An example in Synthetic Model Examples section serves to illustrate this observation. Therefore, for efficiency, we turn off the non-causal branch post-processings in forward modeling and base the tomography solely on equations 1 and 3.

First-break traveltime tomography with the double-square-root eikonal equation