First-break traveltime tomography with the double-square-root eikonal equation

DSR tomography

The first-break traveltime tomography with DSR eikonal equation (DSR tomography) can be established by following a procedure analogous to the traditional one with the shot-indexed eikonal equation (standard tomography). To further reveal their differences, in this section we will derive both approaches.

For convenience, we use slowness-squared $w \equiv 1/v^2$ instead of velocity $v$ in equations 1, 3 and 4. Based on analysis in Appendix A, the velocity model $w (z,x)$ and prestack cube $T (z,r,s)$ are Eulerian discretized and arranged as column vectors $\mathbf{w}$ of size $nz \times nx$ and $\mathbf{t}$ of size $nz \times nx \times nx$. We denote the observed first-breaks by $\mathbf{t}^{obs}$, and use $\mathbf{t}^{std}$ and $\mathbf{t}^{dsr}$ whenever necessary to discriminate between $\mathbf{t}$ computed from shot-indexed eikonal equation and DSR eikonal equation.

The tomographic inversion seeks to minimize the $l_2$ (least-squares) norm of the data residuals. We define an objective function as follows:

$$E (\mathbf{w}) = \frac{1}{2} (\mathbf{t}-\mathbf{t}^{obs})^T (\mathbf{t}-\mathbf{t}^{obs})\;,$$ (5)

where the superscript $T$ represents transpose. A Newton method of inversion can be established by considering an expansion of the misfit function 5 in a Taylor series and retaining terms up to the quadratic order (Bertsekas, 1982):

$$E (\mathbf{w} + \delta \mathbf{w}) = E (\mathbf{w}) + \delta... ...f{w}) \delta \mathbf{w} + O (\vert\delta \mathbf{w}\vert^3)\;.$$ (6)

Here $\nabla_w E$ and $\mathbf{H}$ are gradient vector and Hessian matrix, respectively. We may evaluate the gradient by taking partial derivatives of equation 5 with respect to $\mathbf{w}$, yielding

$$\nabla_w E \equiv \frac{\partial E}{\partial \mathbf{w}} = \mathbf{J}^T (\mathbf{t} - \mathbf{t}^{obs})\;,$$ (7)

where $\mathbf{J}$ is the Frechét derivative matrix and can be found by further differentiating $\mathbf{t}$ with respect to $\mathbf{w}$.

We start by deriving the Frechét derivative matrix of standard tomography. Denoting

$$D_m \equiv \frac{\partial}{\partial m}\;;\,\,\, m = z,x,r,s$$ (8)

as the partial derivative operator in the $m$'s direction, equation 4 can be re-written as

$$D_z t^{std}_k \cdot D_zt^{std}_k + D_x t^{std}_k \cdot D_x t^{std}_k = w\;;\,\,\, k = 1,2,3,...,nx\;.$$ (9)

Here we assume that there are in total $nx$ shots and use $t^{std}_k$ for first-breaks of the $k$th shot. Applying $\partial / \partial w$ to both sides of equation 9, we find

$$J^{std}_k \equiv \frac{\partial t^{std}_k}{\partial w} = \... ... + D_x t^{std}_k \cdot D_x)^{-1}\;;\,\,\, k = 1,2,3,...,nx\;.$$ (10)

Kinematically, each $J^{std}_k$ contains characteristics of the $k$th shot. Because shots are independent of each other, the full Frechét derivative is a concatenation of individual $J^{std}_k$, as follows:

$$J^{std} = \left[ J^{std}_1\;\;\;J^{std}_2\;\;\;\cdots\;\;\;J^{std}_{nx} \right]^T\;.$$ (11)

Inserting equation 11 into equation 7, we obtain

$$\nabla_w E = \sum_{k=1}^{nx} \left(\mathbf{J}^{std}_k\right)^T (\mathbf{t}^{std}_k - \mathbf{t}^{obs}_k)\;,$$ (12)

where, similar to $t^{std}_k$, $t^{obs}_k$ stands for the observed first-breaks of the $k$th shot.

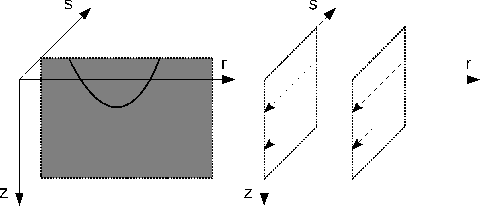
Figure 3 illustrates equation 12 schematically, i.e. the gradient produced by standard tomography. The first step on the left depicts the transpose of the $k$th Frechét derivative acting on the corresponding $k$th data residual. It implies a back-projection that takes place in the $z - r$ plane of a fixed $s$ position. The second step on the right is simply the summation operation in equation 12.

cartonstd
Figure 3. The gradient produced by standard tomography. The solid curve indicates a shot-indexed characteristic.

To derive the Frechét derivative matrix associated with DSR tomography, we first re-write equation 1 with definition 8

$$D_z t^{dsr} = - \sqrt{w_s - D_s t^{dsr} \cdot D_s t^{dsr}} - \sqrt{w_r - D_r t^{dsr} \cdot D_r t^{dsr}}\;,$$ (13)

where $w_s$ and $w_r$ are $w$ at sub-surface source and receiver locations, respectively. Note that in equation 13 $w$ appears twice. Thus a differentiation of $t^{dsr}$ with respect to $w$ must be carried out through the chain-rule:

$$J^{dsr} \equiv \frac{\partial t^{dsr}}{\partial w} = \left.... ...al w_r} \right\vert _{w_s} \frac{\partial w_r}{\partial w}\;.$$ (14)

We recall that $w$ and $t^{dsr}$ are of different lengths. Meanwhile in equation 13, both $w_s$ and $w_r$ have the size of $t^{dsr}$. Clearly in equation 14 $\partial w_s / \partial w$ and $\partial w_r / \partial w$ must achieve dimensionality enlargement. In fact, according to Figure 1, $w_s$ and $w_r$ can be obtained by spraying $w$ such that $w_s (z,r,s) = w (z,s)$ and $w_r (z,r,s) = w (z,r)$. Therefore, $\partial w_s / \partial w$ and $\partial w_r / \partial w$ are essentially spraying operators and their adjoints perform stackings along $s$ and $r$ dimensions, respectively.

In Appendix B, we prove that $J^{dsr}$ has the following form:

$$J^{dsr} = B^{-1} (C_s + C_r)\;.$$ (15)

Combining equations 7 and 15 results in

$$\nabla_w E = \left(\mathbf{C}_s^T + \mathbf{C}_r^T\right) \mathbf{B}^{-T} (\mathbf{t}^{dsr} - \mathbf{t}^{obs})\;.$$ (16)

Note that unlike equation 12, equation 16 can not be expressed as an explicit summation over shots.

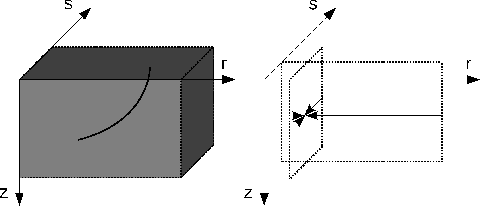
Figure 4 shows the gradient of DSR tomography. Similarly to the standard tomography, the gradient produced by equation 16 is a result of two steps. The first step on the left is a back-projection of prestack data residuals according to the adjoint of operator $B^{-1}$. Because $B$ contains DSR characteristics that travel in prestack domain, this back-projection takes place in $(z,r,s)$ and is different from that in standard tomography, although the data residuals are the same for both cases. The second step on the right follows the adjoint of operators $C_s$ and $C_r$ and reduces the dimensionality from $(z,r,s)$ to $(z,x)$. However, compared to standard tomography this step involves summations in not only $s$ but also $r$.

cartondsr
Figure 4. The gradient produced by DSR tomography. The solid curve indicates a DSR characteristic, which has one end in plane $z = 0$ and the other in plane $s = r$. Compare with Figure 3.

First-break traveltime tomography with the double-square-root eikonal equation