 |
 |
 |
 | OC-seislet: seislet transform construction with differential offset continuation |  |
![[pdf]](icons/pdf.png) |
Next: OC-seislet structure
Up: Theoretical basis
Previous: Theoretical basis
The lifting scheme (Sweldens, 1995) provides a convenient approach
for designing digital wavelet transforms. The general recipe is as
follows:
- Organize the input data as a sequence of records. For
OC-seislet transform of 2-D seismic reflection data, the input
is in the `frequency'-`midpoint wavenumber'-`offset' domain
after the log-stretched NMO correction (Bolondi et al., 1982),
and the transform direction is offset.
- Divide the data records (along the offset axis in the case of the
OC-seislet transform) into even and odd components
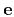 and
and
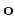 . This step works at one scale level.
. This step works at one scale level.
- Find the residual difference
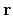 between the odd
component and its prediction from the even component:
between the odd
component and its prediction from the even component:
![$\displaystyle \mathbf{{r}} = \mathbf{{o}} - \mathbf{P[{e}]}\;,$](img13.png) |
(1) |
where
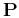 is a prediction operator.
For example, one can obtain Cohen-Daubechies-Feauveau (CDF) 5/3
biorthogonal wavelets (Cohen et al., 1992) by defining the
prediction operator as a linear interpolation between two neighboring
samples,
is a prediction operator.
For example, one can obtain Cohen-Daubechies-Feauveau (CDF) 5/3
biorthogonal wavelets (Cohen et al., 1992) by defining the
prediction operator as a linear interpolation between two neighboring
samples,
![$\displaystyle \mathbf{P[e]}_k = \left(\mathbf{e}_{k-1} + \mathbf{e}_{k}\right)/2\;,$](img15.png) |
(2) |
where 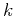 is an index number at the current scale level.
is an index number at the current scale level.
- Find an approximation
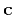 of the data by updating
the even component:
of the data by updating
the even component:
![$\displaystyle \mathbf{{c}} = \mathbf{{e}} + \mathbf{U[{r}]}\;,$](img18.png) |
(3) |
where
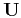 is an update operator. Constructing the
update operator for CDF 5/3 biorthogonal wavelets aims at preserving
the running average of the signal
(Sweldens and Schröder, 1996):
is an update operator. Constructing the
update operator for CDF 5/3 biorthogonal wavelets aims at preserving
the running average of the signal
(Sweldens and Schröder, 1996):
![$\displaystyle \mathbf{U[r]}_k = \left(\mathbf{r}_{k-1} + \mathbf{r}_{k}\right)/4\;.$](img20.png) |
(4) |
- The coarse approximation
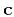 becomes the new data,
and the sequence of steps is repeated on the new data
to calculate the transform coefficients at a coarser scale level.
becomes the new data,
and the sequence of steps is repeated on the new data
to calculate the transform coefficients at a coarser scale level.
Next, we define new prediction and update operators using
offset-continuation operators.
 |
 |
 |
 | OC-seislet: seislet transform construction with differential offset continuation |  |
![[pdf]](icons/pdf.png) |
Next: OC-seislet structure
Up: Theoretical basis
Previous: Theoretical basis
2013-07-26