Bibliography

Aki, K., and P. Richards, 2002, Quantitative seismology (second edition): University Science Books.

Barnes, A. E., 1991, Instantaneous frequency and amplitude at the envelope peak of a constant-phase wavelet: Geophysics, 56, 1058-1060.

Bracewell, R., 1978, The fourier transform and its applications, 2nd ed.: McGraw-HillInc.

Brzostowski, M., and G. McMechan, 1992, 3-D tomographic imaging of near-surface seismic velocity and attenuation: Geophysics, 57, 396-403.

Canales, L., 1984, Random noise reduction: 54th Annual International Meeting, SEG, Expanded Abstracts, 525-527.

Carcione, J. M., 2007, Wave fields in real media: Wave propagation in anisotropic, anelastic, porous and electromagnetic media: Elsevier.

Carcione, J. M., F. Cavallini, F. Mainardi, and A. Hanyga, 2002, Time-domain modeling of constant-Q seismic waves using fractional derivatives: Pure and Applied Geophysics, 159, 1719-1736.

Carmona, R., W. Hwang, and B. Torresani, 1998, Practical time-frequency analysis: Gabor and wavelet transforms with an implementation is s: Academic Press.

Chen, Y., 2017, Fast dictionary learning for noise attenuation of multidimensional seismic data: Geophysical Journal International, 209, no. 1, 21-31.

Chen, Y., and S. Fomel, 2015, Random noise attenuation using local signal-and-noise orthogonalization: Geophysics, 80, WD1-Wd9.

Chen, Y., D. Zhang, Z. Jin, X. Chen, S. Zu, W. Huang, and S. Gan, 2016, Simultaneous denoising and reconstruction of 5D seismic data via damped rank-reduction method: Geophysical Journal International, 206, no. 3, 1695-1717.

Cheng, P., and G. F. Margrave, 2012, Q estimation by a match-filter method: SEG expanded abstracts: 82nd Annual international meeting, 1-6.

Delle Piane, C., J. Sarout, C. Madonna, E. H. Saenger, D. N. Dewhurst, and M. Raven, 2014, Frequency-dependent seismic attenuation in shales: experimental results and theoretical analysis: Geophysical Journal International, 198, 504-515.

Du, J., S. Lin, W. Sun, and G. Liu, 2010, Seismic attenuation estimation using s transform with regularized inversion: 80th Annual International Meeting, SEG, Expanded Abstracts, 2901-2904.

Dutta, G., and G. T. Schuster, 2014, Attenuation compensation for least-squares reverse time migration using the viscoacoustic-wave equation: Geophysics, 79, S251-S262.

Engelhard, L., 1996, Determination of seismic-wave attenuation by complex trace analysis: Geophysical Journal International, 125, 608-622.

Fomel, S., 2007a, Local seismic attributes: Geophysics, 72, A29-A33.

----, 2007b, Shaping regularization in geophysical-estimation problems: Geophysics, 72, R29-R36.

Futterman, W. I., 1962, Dispersive body waves: Journal of Geophysical Research, 67, 5279-5291.

Gan, S., S. Wang, Y. Chen, S. Qu, and S. Zu, 2016, Velocity analysis of simultaneous-source data using high-resolution semblance-coping with the strong noise: Geophysical Journal International, 204, 768-779.

Gao, J., and S. Yang, 2007, On the method of quality factors estimation from zero-offset vsp data: Chines Journal of Geophysics, 50, 1026-1040.

Guo, R., G. Yu, and S. Wang, 2014, A novel method for Q estimating: Beijing 2014 International Geophysical Conference & Exposition, 377-381.

Hauge, P. S., 1981, Measurements of attenuation from vertical seismic profiles: Geophysics, 46, 1548-1558.

Hedlin, K., L. Mewhort, and G. Margrave, 2001, Delineation of steam flood using seismic attenuation: SEG expanded abstracts: 71st Annual international meeting, 1572-1575.

Jannsen, D., J. Voss, and F. Theilen, 1985, Comparison of methods to determine q in shallow marine sediments from vertical reflection seismograms: Geophysical Prospecting, 33, 479-497.

Kjartansson, E., 1979, Constant Q-wave propagation and attenuation: Journal of Geophysical Research Solid Earth, 84, 4737-4748.

Kneib, G., and S. A. Shapiro, 1995, Viscoacoustic wave propagation in 2-d random media and separation of absorption and scattering attenuation: Geophysics, 60, 459-467.

Lawrence, J. F., P. M. Shearer, and G. Masters, 2006, Mapping attenuation beneath north america using waveform cross-correlation and cluster analysis: Geophysical Research Letters, 33, L07315.

Li, H., W. Zhao, H. Zhao, F. Yao, and L. Shao, 2006, Measures of scale based on the wavelet scalogram with applications to seismic attenuation: Geophysics, 71, V111-V118.

Li, J., S. Wang, D. Yang, G. Tang, and Y. Chen, 2018, Subsurface attenuation estimation using a novel hybrid method based on fwe function and power spectrum: Exploration Geophysics, 49, no. 2, 220-230.

Li, Q., H. Zhou, Q. Zhang, H. Chen, and S. Sheng, 2015, Efficient reverse time migration based on fractional laplacian viscoacoustic wave equation: Geophysical Journal International, 204, 488-504.

Matheney, M. P., and R. L. Nowack, 1995, Seismic attenuation values obtained from instantaneous frequency matching and spectral ratios: Geophysical Journal International, 123, 1-15.

Matsushima, J., M. Y. Ali, and F. Bouchaala, 2015, Seismic attenuation estimation from zero-offset vsp data using seismic interferometry: Geophysical Journal International, 204, 1288-1307.

Mousavi, S. M., and C. A. Langston, 2016, Hybrid seismic denoising using higher-order statistics and improved wavelet block thresholding: Bulletin of the Seismological Society of America, 106, no. 4, 1380-1393.

----, 2017, Automatic noise-removal/signal-removal based on general cross-validation thresholding in synchrosqueezed domain and its application on earthquake data: Geophysics, 82, no. 4, V211-V227.

Mousavi, S. M., C. A. Langston, and S. P. Horton, 2016, Automatic microseismic denoising and onset detection using the synchrosqueezed continuous wavelet transform: Geophysics, 81, no. 4, V341-V355.

Prudencio, J., J. M. Ibáñez, A. García-Yeguas, E. Del Pezzo, and A. M. Posadas, 2013, Spatial distribution of intrinsic and scattering seismic attenuation in active volcanic islands-ii: Deception island images: Geophysical Journal International, 195, 1957-1969.

Quan, Y., and J. M. Harris, 1997, Seismic attenuation tomography using the frequency shift method: Geophysics, 62, 895-905.

Raike, S. A., and R. E. White, 1984, Measurements of earth attenuation from downhole and surface seismic recordings: Geophysical Prospecting, 32, 892-919.

Raji, W. O., and A. Rietbrock, 2013, Determination of quality factor (q) in reflection seismic data: SEG expanded abstracts: 83rd Annual international meeting, 3191-3195.

Reine, C., M. van der Baan, and R. Clark, 2009, The robustness of seismic attenuation measurements using fixed- and variable-window time-frequency transforms: Geophysics, 74, WA123-WA135.

Ricker, N., 1953, The form and laws of propagation of seismic wavelets: Geophysics, 18, 10-40.

Ruan, Y., and Y. Zhou, 2010, The effects of 3-d anelasticity (q) structure on surface wave phase delays: Geophysical Journal International, 181, 479-492.

----, 2012, The effects of 3-d anelasticity (q) structure on surface wave amplitudes: Geophysical Journal International, 189, 967-983.

Stockwell, R. G., L. Mansinha, and R. P. Lowe, 1996, Localization of the complex spectrum: The s transform: IEEE Transactions on Signal Processing, 44, 998-1001.

Tonn, R., 1991, The determination of the seismic quality factor q from vsp data: A comparison of different computational methods: Geophysical Prospecting, 39, 1-27.

Toverud, T., and B. Ursin, 2005, Comparison of seismic attenuation models using zero-offset vertical seismic profiling (vsp) data: Geophysics, 70, F17-F25.

Wang, S., D. Yang, J. Li, and H. Song, 2015, Q factor estimation based on the method of logarithmic spectral area difference: Geophysics, 80, V157-V171.

Wang, S.-D., 2011, Attenuation compensation method based on inversion: Applied Geophysics, 8, 150-157.

Wang, Y., 2002, A stable and efficient approach of inverse q filtering: Geophysics, 67, 657-663.

----, 2004, Q analysis on reflection seismic data: Geophysical Research Letters, 31, L17606.

----, 2014, Stable q analysis on vertical seismic profiling data: Geophysics, 79, D217-D225.

Wang, Y., X. Ma, H. Zhou, and Y. Chen, 2018a, L1-2 minimization for exact and stable seismic attenuation compensation: Geophysical Journal International, 213, no. 3, 1629-1646.

Wang, Y., H. Zhou, H. Chen, and Y. Chen, 2018b, Adaptive stabilization for Q-compensated reverse time migration: Geophysics, 83, no. 1, S15-S32.

Wright, C., and D. Hoy, 1981, A note on pulse broadening and anelastic attenuation in near-surface rocks: Physics of the Earth and Planetary interiors, 25, P1-P8.

Yang, S., J. Gao, W. Chen, D. Wang, and B. Weng, 2009, Comparisons of four methods used for seismic quality factors estimation: SEG expanded abstracts: 79th Annual international meeting, 2472-2476.

Zhang, C., and T. J. Ulrych, 2002, Estimation of quality factors from CMP records: Geophysics, 67, 1542-1547.

----, 2007, Seismic absorption compensation: A least squares inverse scheme: Geophysics, 72, R109-R114.

Zhu, T., 2014, Time-reverse modelling of acoustic wave propagation in attenuating media: Geophysical Journal International, 197, 483-494.

----, 2015, Implementation aspects of attenuation compensation in reverse‐time migration: Geophysical Prospecting, 64, 657-670.

Zhu, T., and J. Sun, 2017, Viscoelastic reverse time migration with attenuation compensation: Geophysics, 82, S61-S73.

Appendix A

S transform

For non-stationary data, time-frequency transforms are useful, as they can produce a spectral estimate centered at each time element of the data. In this respect, a 1D data trace is mapped into a 2D spectrogram, which has dimensions of time and frequency (Reine et al., 2009). To introduce the S transform, we first briefly introduce the short-time Fourier transform (STFT).

The STFT is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time

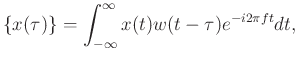$$X_F(\tau,f)= \{x(\tau)\}=\int_{-\infty}^{\infty}x(t)w(t-\tau)e^{-i2\pi ft}dt,$$ (17)

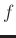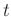where $f$ is the frequency, $\tau$ is a parameter that controls the position of the window function along the $t$ axis.

The STFT might be the most recognized time-frequency transform. It can be understood in such way that the data trace $x$ is gated by a sliding window function $w$, and the Fourier transform (Bracewell, 1978). The sliding window function is commonly chosen as a Hanning window or Gaussian window.

When $w(t)$ is chosen as a Gaussian window function:

$$w(t)=e^{-t^2/2\sigma^2},$$ (18)

where $\sigma$ is the distribution width, the STFT transforms to the definition of Gabor transform (Carmona et al., 1998).

The S transform was proposed by Stockwell et al. (1996) as an extension to the Morlet wavelet transform. Instead of a fixed time length for each frequency in the window functions chosen for STFT, the S transform analyzes shorter data segments as the frequencies increase. Related with the Gaussian window function as shown in equation A-2, the distribution width $\sigma$ is substituted with:

$$\sigma=\frac{1}{\vert f\vert}.$$ (19)

Besides, the Gaussian window function used in the S transform is normalized with respect to the amplitude. Thus, the width of the Gaussian window scales inversely with frequency and amplitude scales linearly with the frequency:

$$w(t,f)=\frac{\vert f\vert}{\sqrt{2\pi}}e^{-t^2f^2/2}.$$ (20)

Combining equation A-1 with equation A-4 we can obtain the definition of the S transform (ST):

$$X_S(\tau,f)= \{x(\tau)\}=\frac{\vert f\vert}{2\pi}\int_{-\infty}^{\infty}x(t)e^{-(t-\tau)^2f^2/2}e^{-i2\pi ft}dt.$$ (21)

The S transform use a frequency-dependent window similar to that of wavelet transform, which allows a better resolution of low frequency components and enables a better time resolution of high frequency components.