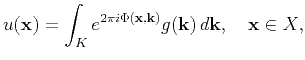|
 |
 |
 | A fast butterfly algorithm for generalized Radon transforms |  |
![[pdf]](icons/pdf.png) |
Next: Low-rank approximations
Up: A fast butterfly algorithm
Previous: Introduction
Assume  is a function in the data space. The hyperbolic Radon transform
is a function in the data space. The hyperbolic Radon transform  maps
maps  to a function
to a function
 in the model space (Thorson and Claerbout, 1985) through
in the model space (Thorson and Claerbout, 1985) through
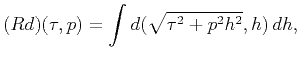 |
(1) |
where  is time,
is time,  is offset,
is offset,  is intercept time, and
is intercept time, and  is slowness. Fixing
is slowness. Fixing  , hyperbola
, hyperbola
 describes the traveltime for the event; hence integration along these curves can be used to identify different reflections.
describes the traveltime for the event; hence integration along these curves can be used to identify different reflections.
Instead of approximating the integral in equation 1 directly, we reformulate it as a double integral,
 |
(2) |
Here  is the frequency,
is the frequency,
 is the Fourier transform of
is the Fourier transform of  in
in  . A simple discretization of equation 2 yields
. A simple discretization of equation 2 yields
 |
(3) |
(the area element is omitted; the same symbols  ,
,  ,
,  , and
, and  are used for both continuous and discrete variables). The reason that hyperbolic RT is harder to compute than linear RT (
are used for both continuous and discrete variables). The reason that hyperbolic RT is harder to compute than linear RT ( ) or parabolic RT (
) or parabolic RT (
 ) should be clear from equation 3: product
) should be clear from equation 3: product  in the phase cannot be decoupled from other terms.
in the phase cannot be decoupled from other terms.
To construct the fast algorithm, we first perform a linear transformation to map all discrete points in  and
and  domains to points in the unit square
domains to points in the unit square
![$ [0,1]\times[0,1]$](img69.png) (
(
![$ [a,b]\times[c,d]$](img70.png) represents a 2D rectangular domain in the
represents a 2D rectangular domain in the  -plane with
-plane with ![$ x\in[a,b]$](img72.png) and
and ![$ y\in[c,d]$](img73.png) ), i.e., a point
), i.e., a point
 min
min max
max![$ ]\times[h_$](img76.png) min
min max
max![$ ]$](img78.png) is mapped to
is mapped to
![$ \mathbf{k}=(k_1,k_2)\in[0,1]\times[0,1]=K$](img79.png) via
via
a point
 min
min max
max![$ ]\times[p_$](img89.png) min
min max
max![$ ]$](img78.png) is mapped to
is mapped to
![$ \mathbf{x}=(x_1,x_2)\in[0,1]\times[0,1]=X$](img91.png) via
via
If we define input
 , output
, output
 , and phase function
, and phase function
 , then equation 3 can be written as
, then equation 3 can be written as
 |
(6) |
(throughout the paper,  and
and  will either be used for sets of discrete points or square domains containing them; the meaning should be clear from the context). This form is the discrete version of an oscillatory integral of the type
will either be used for sets of discrete points or square domains containing them; the meaning should be clear from the context). This form is the discrete version of an oscillatory integral of the type
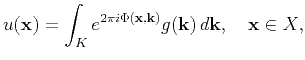 |
(7) |
whose fast evaluation has been considered in Candès et al. (2009). Our method for computing the summation in equation 6 follows the FIO butterfly algorithm introduced there.
Subsections
 |
 |
 |
 | A fast butterfly algorithm for generalized Radon transforms |  |
![[pdf]](icons/pdf.png) |
Next: Low-rank approximations
Up: A fast butterfly algorithm
Previous: Introduction
2013-07-26
![]() is a function in the data space. The hyperbolic Radon transform
is a function in the data space. The hyperbolic Radon transform ![]() maps
maps ![]() to a function
to a function
![]() in the model space (Thorson and Claerbout, 1985) through
in the model space (Thorson and Claerbout, 1985) through
![]() and
and ![]() domains to points in the unit square
domains to points in the unit square
![]() (
(
![]() represents a 2D rectangular domain in the
represents a 2D rectangular domain in the ![]() -plane with
-plane with ![]() and
and ![]() ), i.e., a point
), i.e., a point
![]() min
min![]() max
max![]() min
min![]() max
max![]() is mapped to
is mapped to
![]() via
via