 |
 |
 |
 | A fast butterfly algorithm for generalized Radon transforms |  |
![[pdf]](icons/pdf.png) |
Next: Butterfly structure
Up: Algorithm
Previous: Algorithm
Clearly the range and possibly other factors such as gradient of phase
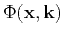 determine the degree of oscillations in the kernel
determine the degree of oscillations in the kernel
 . Let
. Let  be an integer power of two, which is on the order of the maximum value of
be an integer power of two, which is on the order of the maximum value of
 for
for
 and
and
 (the exact choice of
(the exact choice of  depends on the desired efficiency and accuracy of the algorithm, which will be made specific in numerical examples). The design of the fast algorithm relies on the key observation that the kernel
depends on the desired efficiency and accuracy of the algorithm, which will be made specific in numerical examples). The design of the fast algorithm relies on the key observation that the kernel
 , when properly restricted to subsets of
, when properly restricted to subsets of  and
and  , admits accurate and low-rank separated approximations. More precisely, if
, admits accurate and low-rank separated approximations. More precisely, if 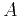 and
and  are two square boxes in
are two square boxes in  and
and  , with sidelengths
, with sidelengths  ,
,  obeying
obeying
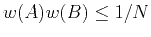 -- in which case the pair
-- in which case the pair 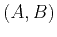 is called admissible -- then
is called admissible -- then
 for for |
(8) |
where
 is independent of
is independent of  for a fixed error
for a fixed error 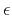 . Here and below the subscript
. Here and below the subscript  is slightly abused:
is slightly abused:  should be understood as multi-indices
should be understood as multi-indices  , and accordingly
, and accordingly
 is the total number of terms in a double sum. Furthermore, Candès et al. (2009) showed that this low-rank approximation can be constructed via a tensor-product Chebyshev interpolation of
is the total number of terms in a double sum. Furthermore, Candès et al. (2009) showed that this low-rank approximation can be constructed via a tensor-product Chebyshev interpolation of
 in the
in the
 variable when
variable when
 , and in the
, and in the
 variable when
variable when
 .
.
Specifically, when
 ,
,
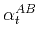 and
and
 are given by
are given by
| |
|
 |
(9) |
| |
|
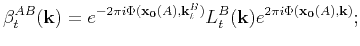 |
(10) |
and when
 ,
,
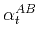 and
and
 are given by
are given by
| |
|
 |
(11) |
| |
|
 |
(12) |
Boldface letters
 ,
,
 denote 2D vectors.
denote 2D vectors.
 is a point on the 2D,
is a point on the 2D,
 Chebyshev grid in box
Chebyshev grid in box  centered at
centered at
 , i.e., let
, i.e., let
 ,
,
 , then
, then
| |
|
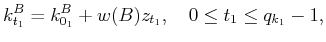 |
(13) |
| |
|
 |
(14) |
where
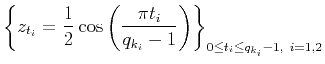 |
(15) |
is the 1D Chebyshev grid of order  on
on
![$ [-1/2,1/2]$](img133.png) . See Figure 1 for an illustration.
. See Figure 1 for an illustration.
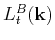 is the 2D Lagrange interpolation defined on the Chebyshev grid:
is the 2D Lagrange interpolation defined on the Chebyshev grid:
 |
(16) |
Analogously,
 is a point on the 2D,
is a point on the 2D,
 Chebyshev grid in box
Chebyshev grid in box 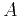 centered at
centered at
 , and
, and
 is the 2D Lagrange interpolation defined on this grid. Based on the discussion above, the number
is the 2D Lagrange interpolation defined on this grid. Based on the discussion above, the number
 in low-rank approximation 8 is equal to
in low-rank approximation 8 is equal to
 when
when
 , and
, and
 when
when
 .
.

|
|---|
grid
Figure 1. A 2D,
 (
( ,
,  ) Chebyshev grid in box
) Chebyshev grid in box  .
.
 is the center of the box.
is the center of the box.
 is a point on the grid.
is a point on the grid.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png)
|
|---|
A simple way of viewing expressions 9 - 12 is: when
 , plugging expression 9 into approximation 8 (leaving
, plugging expression 9 into approximation 8 (leaving
 as it is) yields
as it is) yields
 for for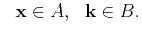 |
(17) |
For fixed
 , the right hand side of equation 17 is just a special interpolation of function
, the right hand side of equation 17 is just a special interpolation of function
 in variable
in variable
 , where
, where
 are the interpolation points,
are the interpolation points,
 are the basis functions. Likewise, when
are the basis functions. Likewise, when
 , plugging expression 12 into approximation 8, we get
, plugging expression 12 into approximation 8, we get
 for for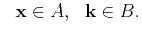 |
(18) |
For fixed
 , the right hand side of equation 18 is a special interpolation of
, the right hand side of equation 18 is a special interpolation of
 in variable
in variable
 :
:
 are the interpolation points,
are the interpolation points,
 are the basis functions.
are the basis functions.
Once the low-rank approximation 8 is known, computing the partial sum
 |
(19) |
generated by points
 inside a box
inside a box  becomes
becomes
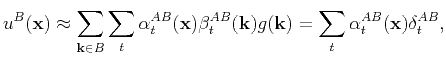 for for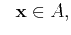 |
(20) |
where
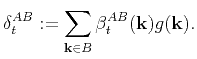 |
(21) |
The case that the box  represents the whole domain
represents the whole domain  is of particular interest, since it corresponds to the original problem. Therefore, if we can find the set of interaction coefficients
is of particular interest, since it corresponds to the original problem. Therefore, if we can find the set of interaction coefficients
 relative to all admissible couples of boxes
relative to all admissible couples of boxes 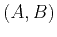 with
with  , our problem will be solved.
, our problem will be solved.
 |
 |
 |
 | A fast butterfly algorithm for generalized Radon transforms |  |
![[pdf]](icons/pdf.png) |
Next: Butterfly structure
Up: Algorithm
Previous: Algorithm
2013-07-26
![]() determine the degree of oscillations in the kernel
determine the degree of oscillations in the kernel
![]() . Let
. Let ![]() be an integer power of two, which is on the order of the maximum value of
be an integer power of two, which is on the order of the maximum value of
![]() for
for
![]() and
and
![]() (the exact choice of
(the exact choice of ![]() depends on the desired efficiency and accuracy of the algorithm, which will be made specific in numerical examples). The design of the fast algorithm relies on the key observation that the kernel
depends on the desired efficiency and accuracy of the algorithm, which will be made specific in numerical examples). The design of the fast algorithm relies on the key observation that the kernel
![]() , when properly restricted to subsets of
, when properly restricted to subsets of ![]() and
and ![]() , admits accurate and low-rank separated approximations. More precisely, if
, admits accurate and low-rank separated approximations. More precisely, if ![]() and
and ![]() are two square boxes in
are two square boxes in ![]() and
and ![]() , with sidelengths
, with sidelengths ![]() ,
, ![]() obeying
obeying
![]() -- in which case the pair
-- in which case the pair ![]() is called admissible -- then
is called admissible -- then
![]() ,
,
![]() and
and
![]() are given by
are given by
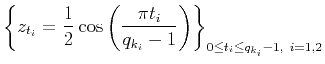


![]() , plugging expression 9 into approximation 8 (leaving
, plugging expression 9 into approximation 8 (leaving
![]() as it is) yields
as it is) yields